МАЛЫЙ МЕХМАТ МГУ

Кружок 6 класса

Занятие 1. Задачи для знакомства

1.

Преподаватели собрали письменные работы и пересчитывают их перед проверкой. Ирина Сергеевна сложила их стопками по сто работ. Даниил Алексеевич может за две секунды отсчитать пять работ. За какое наименьшее время он может отсчитать себе 75 работ для проверки?

Ответ Решение

Ответ. За 10 секунд.

Решение. Даниил Алексеевич может взять стопку, в которой 100 работ, отсчитать 25 работ (для этого нужно (25 : 5) · 2 = 10 секунд) и отложить в сторону, а оставшиеся 75 работ из этой стопки забрать себе на проверку.

2.

а)

Разрежьте какой-нибудь квадрат на четыре равные части.

б)

А теперь разрежьте такой же квадрат на 16 равных частей.

в)

Сможете ли вы разрезать такой же квадрат на 17 равных частей?

Ответ

Ответ. Решения пунктов а, б, в:

3.

а)

Предложите набор из трёх гирек, каждая из которых весит целое число граммов, чтобы с их помощью на чашечных весах без делений можно было взвесить любой целочисленный вес от 1 до 7 граммов.

б)

Не хватит ли для этой цели набора из каких-нибудь двух гирек (не обязательно с целочисленными массами)?

Ответ Решение

Ответ. а) Например, 1г, 2г и 4г; б) не хватит.

Решение.

а) С помощью гирек в 1г, 2г и 4г можно также взвесить: 3г = 1г + 2г, 5г = 1г + 4г, 6г = 2г + 4г, 7г = 1г + 2г + 4г.

б) Имея гирьки весов a и b (будем считать, что a > b), можно взвесить только массы a, b, a + b и a − b (в последнем случае гирьки надо класть на разные чашки весов). А нам нужно взвесить 7 различных масс — от 1 г до 7 г. Так что двух гирек нам заведомо не хватит (даже если использовать гирьки с дробным весом).

4.

В аудиториях 404 и 405 писали письменную работу по 30 шестиклассников. Проверив их работы, Андрей Михайлович сказал коллегам: «В этих двух аудиториях вместе решивших шестую задачу на пять человек меньше, чем не решивших её». Докажите, что Андрей Михайлович что-то напутал.

Решение

Решение.

Способ I. Предположим сначала, что шестую задачу решило чётное число человек. Тогда не решило её на 5 человек больше, то есть уже нечётное число. Общее число школьников, писавших письменную работу в двух аудиториях, в этом случае будет нечётным (как сумма чётного и нечётного чисел). Но в двух аудиториях было 30·2 = 60 человек, то есть чётное число. Получаем противоречие. Аналогичным образом мы придём к противоречию, предположив, что шестую задачу решило нечётное число человек.

Способ II. Пусть в этих двух аудиториях было n человек, решивших шестую задачу, тогда не решивших её там было n+5 человек. А всего в двух аудиториях письменную работу писали 30·2 = 60 человек. Составим уравнение: n+n+5 = 60, откуда 2n = 55. Так как n — целое число, в левой части равенства стоит чётное число, а в правой — нечётное, чего быть не может. Следовательно, Андрей Михайлович что-то напутал.

5.

В корзине лежат 30 рыжиков и груздей. Среди любых 12 грибов имеется хотя бы один рыжик, а среди любых 20 грибов имеется хотя бы один груздь. Сколько рыжиков и сколько груздей в корзине?

Ответ Решение

Ответ. 11 груздей и 19 рыжиков.

Решение. Из первого условия следует, что груздей не больше 11. В самом деле, если бы их было хотя бы 12, то среди этих 12 грибов не было бы рыжиков, что противоречит условию задачи. Аналогичным образом из второго условия следует, что рыжиков не более 19. Таким образом, всего грибов в корзине не больше 30. Ровно 30 их будет, только если груздей 11, а рыжиков 19.

6.

Может ли быть верным равенство К×О×Т = У×Ч×Ё×Н×Ы×Й, если в него вместо букв подставить цифры от 0 до 9? Разные буквы соответствуют разным цифрам. Буква О не обязательно соответствует цифре 0.

Ответ Решение

Ответ. Не может.

Решение.

Рассмотрим два случая.

Первый случай: одна из букв соответствует цифре 0. Так как все буквы разные и соответствуют разным цифрам, ноль может оказаться только в одной из частей равенства. Тогда в этой части равенства произведение будет равно нулю, а в другой — нет. Получаем неверное равенство.

Второй случай: ни одна из букв не соответствует цифре 0. Тогда каждой цифре от 1 до 9 соответствует какая-то одна буква. В частности, какая-то одна буква соответствует цифре 7. В той части равенства, где находится эта буква, произведение будет делиться на 7, а в другой — нет. Снова получаем неверное равенство.

Замечание. При рассмотрении второго случая можно рассуждать и иначе. Постараемся заменить буквы цифрами так, чтобы в левой части произведение было как можно больше, а в правой — как можно меньше. Для этого заменим К×О×Т = 7×8×9 = 504 (выбираем три самые большие цифры) и У×Ч×Ё×Н×Ы×Й = 1×2×3×4×5×6 = 720. При такой подстановке цифр вместо букв произведение в левой части оказывается меньше произведения в правой части. Нетрудно видеть, что то же самое будет происходить и при любой другой подстановке. Поэтому верного равенства быть не может.

7.

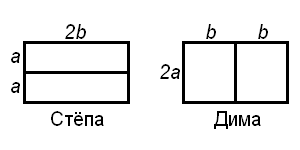
Дима разрезал прямоугольник на два прямоугольника с периметрами по 40 см, а Стёпа разрезал точно такой же прямоугольник на два прямоугольника с периметрами по 50 см. Найдите длины сторон исходного прямоугольника.

Ответ Решение

Ответ. 10 см и 20 см.

Решение.

На рисунке показано два способа разрезать один и тот же прямоугольник на два равных прямоугольника. (Убедитесь самостоятельно, что если прямоугольник разрезать на два прямоугольника с одинаковым периметром, то эти прямоугольники окажутся равными.) Обозначим половинку одной из сторон исходного прямоугольника через а, а вторую — через b (см. рисунок). Дима разрезал прямоугольник на два прямоугольника со сторонами 2а и b, а Стёпа — на два прямоугольника со сторонами а и 2b. Из условия получаем уравнения: 2·(2a + b) = 40 и 2·(a + 2b) = 50. Сложив эти два уравнения, получим: 2·(3a + 3b) = 90, или 6·(a + b) = 90, откуда a + b = 15. Вспоминая, что 2·(2a + b) = 40, откуда 2a + b = 20, легко найдём, что a = 5, а затем — что b = 10. А стороны исходного прямоугольника равны 2a = 10 см и 2b = 20 см.

8.

По данным опроса, проведенного в 6 "Ё" классе, пятая часть учеников, интересующихся математикой, интересуются еще и биологией, а четверть учеников, интересующихся биологией, интересуются также и математикой. И только Олегу и Паше не интересен ни один из этих предметов. Сколько человек в 6 "Ё" классе, если известно, что их больше 20, но меньше 30?

Ответ Решение

Ответ. 26 человек.

Решение. Интересующихся только математикой вчетверо больше интересующихся обоими предметами; интересующихся только биологией втрое больше интересующихся обоими предметами. Значит, число тех, кто интересуется хотя бы одним из двух предметов, должно делиться на 8 (всех вместе их в 8 раз больше, чем интересующихся обоими предметами). 8 и 16 — мало, так как 16 + 2 = 18 < 20 (не забудем посчитать Олега и Пашу); 32, 40 и т.д. — много; 24 подходит. Итак, в классе 24 человека, которые интересуются математикой или биологией (а может быть, и тем, и другим), а ещё есть Олег и Паша. Таким обраом, всего в классе 24 + 2 = 26 человек.

9.

Бился Иван-Царевич со Змеем Горынычем, трёхглавым и трёххвостым. Одним ударом он мог срубить либо одну голову, либо один хвост, либо две головы, либо два хвоста. Но, если срубить один хвост, то вырастут два; если срубить два хвоста — вырастет голова; если срубить голову, то вырастает новая голова, а если срубить две головы, то не вырастет ничего. Как должен действовать Иван-Царевич, чтобы срубить Змею все головы и все хвосты как можно быстрее?

Ответ Решение

Ответ. Это можно сделать за 9 ударов. Например, так: (3, 3) → (4, 3) → (5, 3) → (6, 3) → (4, 4) → (2, 5) → (6, 0) → (4, 0) → (2, 0) → (0, 0). (Каждая пара чисел — это число голов и хвостов, оставшихся у Змея после очередного удара с учётом тех хвостов и голов, которые только что выросли.)

Решение.

Способ отрубить Змею все головы и хвосты за 9 ударов приведён в ответе. Теперь докажем, что этого нельзя сделать за меньшее число ударов.

Иван-Царевич может использовать удары трёх типов:
А) отрубить два хвоста, вырастет одна голова;
В) отрубить две головы;
С) отрубить один хвост, вырастет два хвоста (по сути — просто добавить один хвост).
Отрубать одну голову бесполезно, поэтому такие удары использовать не будем.

1. Число ударов типа А должно быть нечётным. В самом деле, только при таких ударах меняется чётность числа голов. А чётность числа голов должна измениться: сначала их было 3, а в конце должно остаться 0. Если же таких ударов сделать чётное число, число голов останется нечётным (и значит, не будет равно нулю).
2. Так как только ударами типа А можно уменьшить число хвостов, одного такого удара не хватит. Поэтому таких ударов должно быть не меньше двух, а с учётом предыдущего пункта их должно быть хотя бы три.
3. После трёх ударов типа А вырастет три новых головы, и всего нужно будет отрубить 6 голов. Для этого потребуется хотя бы 3 удара типа В.
4. Чтобы отрубить 3 раза по два хвоста ударами типа А, нужно иметь 6 хвостов. Для этого нужно «вырастить» три дополнительных хвоста, сделав 3 удара типа С.
Итак, нужно сделать не менее трёх ударов каждого из указанных типов; всего — не менее 9 ударов.