МАЛЫЙ МЕХМАТ МГУ

Кружок 6 класса

Занятие 18. Графы

Знакомство с графами

1.

Волшебная страна Фарг почти вся состоит из непреодолимых гор и рек. В ней есть шесть городов: А, Б, В, Г, Д и Е. Известно, что из А проложены дороги в Б и Г, из Б — в А, Г и Д, из В — в Г и Е, из Г — в В и Д, из Д — в Б и Г, из Е — только в В. Все остальные дороги непроходимы.

а)

Нарисуйте карту страны Фарг.

б)

Нарисуйте карту так, чтобы дороги не пересекались.

в)

Может ли житель города А попасть в город Д, если ему нельзя проходить через Г?

г)

Сможет ли он при тех же условиях попасть в город Е?

Решение

Ре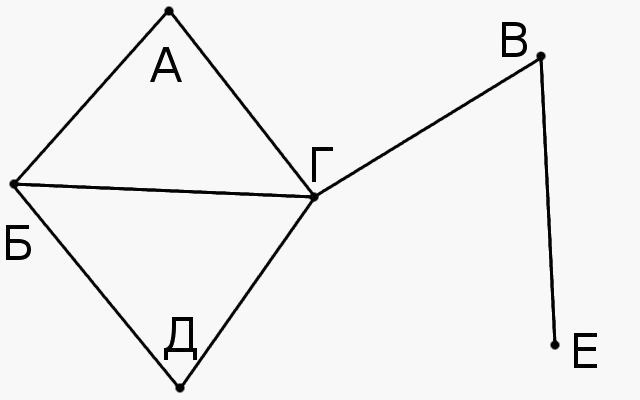шение. а, б)

в) Может: А → Б → Д.
г) Не сможет: если запретить проходить через город Г, города Е и В перестают соединятся с городами А, Б и Д.

• у них равное число вершин;
• вершины каждого графа можно пронумеровать так, что если вершины с номерами i и j соединены ребрами в одном графе, то вершины с теми же номерами соединены таким же числом рёбер и в другом графе, а если вершины с номерами i и j не соединены ребром в одном графе, то вершины с теми же номерами не соединены и в другом графе.

2.

Найдите все наборы одинаковых графов:

Ответ Решение

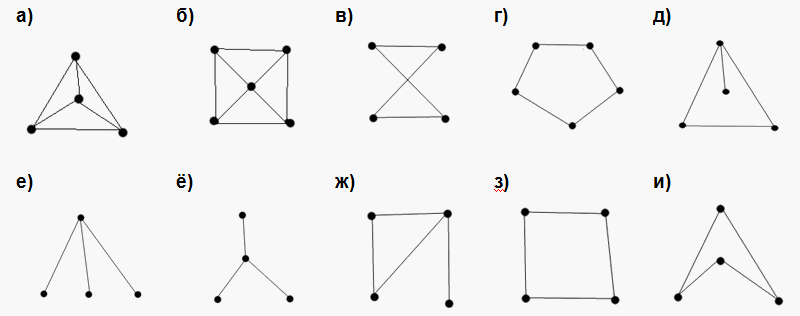Ответ. В = З = И, Д = Ж, Е = Ё.

Решение.

Посчитаем для каждого графа пару чисел: число его вершин и число его рёбер. Если у графов отличается число вершин или число рёбер, то они не могут быть одинаковыми.

Графы Б и Г отличаются от остальных числом вершин (у них по 5 вершин, а у остальных по 4) и друг от друга числом рёбер. Поэтому они ни с кем больше не одинаковые.

Из оставшихся графов только у графа А 6 ребёр, поэтому он тоже ни с кем не одинаковый.

У графов Е и Ё по 4 вершины и по 3 ребра. Легко проверить, что они одинаковые.

У оставшихся графов В, Д, Ж, З, И по 4 вершины и по 4 ребра. Но у них разные степени вершин: у графов В, З, И степени всех вершин равны 2, а у графов Д и Ж по две вершины степени 2 и по одной вершине степеней 1 и 3. Легко убедиться, что В=З=И и Д=Ж, но В≠Д. Таким образом, мы перечислили все наборы одинаковых графов и доказали, что других нет.

3.

Найдите количество:

а)

графов с двумя вершинами;

б)

графов с тремя рёбрами;

в)

связных графов с тремя рёбрами;

г)

несвязных графов с четырьмя вершинами.

Решение

Ре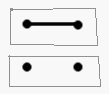шение. а) 2:

б) Таких графов бесконечно много: к любому связному графы с тремя рёбрами (см. пункт в)) можно добавить неограниченное число отдельных вершин.
в) 3:

г) 5: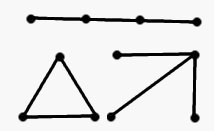

Кёнигсбергские мосты

4.

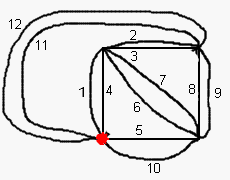
Можно ли начертить данные графы одним росчерком (не отрывая руки от бумаги и не проходя по ребру дважды)?

Ответ Решение

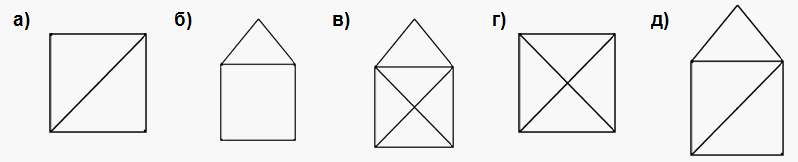Ответ. а, б, в, д) Можно; г) нельзя.

Решение.

а, б, в, д) На рисунке ниже показано, как можно нарисовать каждый из этих графов одним росчерком. Последовательность и направление обхода показаны цифрами и стрелками:

Обратите внимание: если в графе есть нечётная вершина, обход должен начинаться или заканчиваться в ней. Если нечётных вершин две, то обход начинается в одной из них и заканчивается в другой. Почему так должно происходить, объясняет решение задачи 5.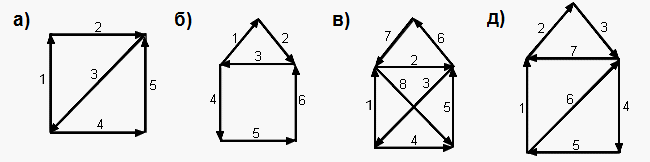

г) В графе из пункта г есть четыре вершины нечётной степени 3, поэтому в силу задачи 5 его нельзя нарисовать одним росчерком.

5.

Докажите, что граф с более чем двумя вершинами нечётной степени невозможно начертить одним росчерком (не отрывая ручки от бумаги и не проводя никакое ребро дважды).

Решение

Решение. Представим, что мы обводим граф и пройденные рёбра выкидываем. Когда мы проходим через вершину (то есть сначала входим в неё по одному ребру, а потом выходим по другому), её степень уменьшается на 2. Значит, степени всех вершин сохраняют чётность. Когда мы закончим обводить граф, степени всех вершин должны оказаться равны нулю (ведь мы выкинем все рёбра). Поэтому нечётная степень может быть только у первой и последней вершины: их степени будут уменьшаться на 1, соответственно, в самом начале и в самом конце обхода.

6.

Дана проволока длиной 12 см. Можно ли сложить из нее каркас куба с ребром в 1 см? Проволоку нельзя резать.

Ответ Решение

Ответ. Нельзя.

Решение.

У куба 12 рёбер по 1 см, а у нас есть ровно 12 см проволоки. Значит, делать двойные рёбра нельзя, иначе нам не хватит проволоки.

Каркас куба можно изобразить в виде графа:

Если бы каркас можно было сложить из проволоки, не разрезая её, то и граф можно было бы нарисовать, не отрывая карандаша от бумаги (рисуя рёбра в том порядке, в котором мы делаем их из проволоки). А это невозможно в силу предыдущей задачи: ведь у этого графа целых восемь вершин степени 3.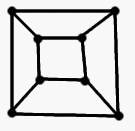

Разные задачи

7.

Докажите, что среди любых шести человек обязательно найдутся либо три попарно знакомых, либо три попарно незнакомых.

Решение

Решение.

Рассмотрим одного из этих шестерых. Назовём его А. Среди остальных пяти у него обязательно есть либо трое знакомых, либо трое незнакомых.

Сначала рассмотрим случай, когда А знаком по крайней мере с тремя другими: B, C и D. Если хоть какие-то двое из этих троих знакомы между собой (например, В и С), то мы получаем тройку попарно знакомых людей А, В, С. Если же они все незнакомы между собой, то мы получаем тройку попарно незнакомых: B, C и D.

Аналогично рассматривается случай, когда А не знаком по крайней мере с тремя другими (назовём их снова B, C и D). Если хоть какие-то двое из этих троих не знакомы между собой (например, В и С), то мы получаем тройку попарно незнакомых людей А, В, С. Если же они все знакомы между собой, то мы получаем тройку попарно знакомых: B, C и D.

8.

Пешеход обошел шесть улиц одного города, пройдя каждую ровно два раза, но не смог обойти их, пройдя каждую лишь один раз. Могло ли такое быть, если в городе нет тупиков?

Ответ Решение

Ответ. Могло. Годится, например, город с такой картой:

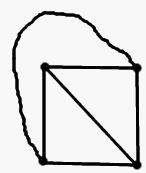Решение.

Докажем, что город с картой, приведённой в ответе, удовлетворяет условию задачи.

Сначала докажем, что улицы этого города нельзя обойти, пройдя каждую по одному разу. Если бы это было возможно, то и граф, изображающий карту города, можно было бы нарисовать одним росчерком (просто рисуя соответствующий маршрут обхода улиц). А этого сделать нельзя в силу задачи 5: в этом графе все четыре вершины имеют нечётную степень 3.

Следующий рисунок показывает, как можно обойти улицы этого города, пройдя каждую по два раза. Для наглядности мы изображаем каждую улицу двумя рёбрами и показываем цифрами порядок обхода улиц. Красной точкой отмечено начало и конец маршрута.

P.S. Автор этого текста, к сожалению, очень плохо рисует, так что не судите строго :)