МАЛЫЙ МЕХМАТ МГУ

Кружок 9-11 классов

Занятие 18 (19 февраля 2011 года). Комбинаторика-2

1.

В школьной столовой 5 кранов для умывания. Каждый может быть закрыт или открыт. Сколькими способами может течь вода в столовой?

2.

Сколько разных слов (не только осмысленных) можно получить, переставляя буквы в словах

а)

РОК;

б)

КУРОК;

в)

КОЛОБОК;

г)

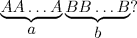
3.

Сколько существует пар 5-значных чисел, в которых числа имеют хотя бы две одинаковые цифры?

4.

а)

В заборе 20 досок, каждую надо покрасить в синий, зелёный или жёлтый цвет, причём соседние доски красятся в разные цвета. Сколькими способами это можно сделать?

б)

А если требуется ещё, чтобы хоть одна из досок обязательно была синей?

5.

а)

Сколько существует 10-значных чисел, не содержащих цифру 1?

б)

Сколько из них содержит цифру 9 (хотя бы одну)?

6.

Найдите коэффициенты при x¹⁷ и x¹⁸ после раскрытия скобок и приведения подобных членов в выражении (1 + x⁵ + x⁷)²⁰.

7.

В ряду 1 + 1 + ... + 1 из 105 единиц изменили знак на противоположный перед каждой третьей единицей, затем — перед каждой пятой, а затем — перед каждой седьмой. Найдите значение полученного выражения.

8.

Некоторое число делится на 2, но не делится на 4. Докажите, что количество четных делителей этого числа равно количеству его нечетных делителей.

9.

Какое наибольшее количество непересекающихся диагоналей можно провести в выпуклом а) 8-угольнике; б) n-угольнике (две диагонали, имеющие общую вершину считаются непересекающимися)?