МАЛЫЙ МЕХМАТ МГУ

Кружок 9-11 классов

Занятие 16 (29 января 2011 года). Теория чисел-1

1.

Можно ли с помощью циркуля и линейки разделить угол 19° на 19 равных частей?

2.

a)

Найдите НОД(248658,345492) (для арифметических действий можно использовать калькулятор).

б)

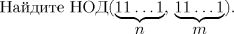
в)

Найдите НОД(a^m − 1,aⁿ − 1).

3.

Найдите наименьшее натуральное n, для которого 2011! не делится на 34ⁿ.

4.

Сколько различных делителей имеют числа

а)

2·3·5;

б)

2·3·5·7·11;

в)

2²·3³·5⁵· 7⁷· 11¹¹?

5.

На доске написано 10 плюсов и 15 минусов. Разрешается стереть любые два знака и написать вместо них плюс, если они одинаковы, и минус в противном случае. Какой знак останется на доске после выполнения 24 таких операций?

6.

Пусть p > 3 — простое число. Докажите, что p² − 1 делится на 24.

7.

Дан многочлен с целыми коэффициентами. Если в него вместо неизвестной подставить 2 или 3, то получаются числа, делящиеся на 6. Докажите, что если вместо неизвестной в него подставить 5, то также получится число, делящееся на 6.

8.

Разочарованный вкладчик фонда «МММ» разорвал акцию на 8 кусков. Не удовлетворившись этим, он разорвал один из кусков еще на 8, и т. д. Могло ли у него получиться 2011 кусков?

9.

Дано простое p.

a)

Найдите все такие натуральные числа, меньшие p, которые являются решением уравнения x² ≡ 1 (mod p).

б)

Докажите, что (p − 1)! ≡ −1 (mod p).

в)

Докажите, что если (n − 1)! ≡ −1 (mod n), то n — простое.

10.

В Лесогории живут только эльфы и гномы. Гномы лгут, говоря про своё золото, а в остальных случаях говорят правду. Эльфы лгут, говоря про гномов, а в остальных случаях говорят правду. Однажды два лесогорца сказали:
А: Всё моё золото я украл у Дракона.
Б: Ты лжешь.
Определите, эльфом или гномом является каждый из них.

11.

На столе лежат в ряд пять монет: средняя — вверх орлом, а остальные — вверх решкой. Разрешается одновременно перевернуть три рядом лежащие монеты. Можно ли при помощи нескольких таких переворачиваний все пять монет положить вверх орлом? А решкой?