МАЛЫЙ МЕХМАТ МГУ

Кружок 7 класса

Занятие 19. Циклы в графах (24.03.2007)

Путь в графе – это последовательность рёбер, в которой конец каждого ребра (кроме последнего) совпадает с началом следующего.

Замкнутый путь называется циклом. Простым циклом называется цикл без самопересечений.

1.

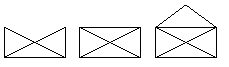Какие из фигур, изображённых на рисунке, можно нарисовать, не отрывая карандаша от бумаги и проводя каждую линию только один раз?

2.

а)

Докажите, что если в графе существует путь, проходящий по каждому ребру ровно один раз (эйлеров путь), то в этом графе не более двух нечётных вершин.

б)

Докажите, что если в графе существует цикл, проходящий по каждому ребру ровно один раз (эйлеров цикл), то в этом графе нет нечётных вершин – все вершины чётны.

3.

(Лемма о хороводах.) В некоторой компании у каждого человека есть ровно двое друзей. Докажите, что если каждый возьмётся за руки со своими друзьями, то образуется один или несколько хороводов. (Другими словами, если в графе степень каждой вершины равна 2, то граф состоит из одного или нескольких простых циклов.)

4.

В футбольном турнире участвует 20 команд. После того, как все команды провели по две игры, организаторы турнира решили разбить их на три дивизиона, но так, чтобы в одном дивизионе не было команд, уже игравших друг с другом. Всегда ли они смогут это сделать?

5.

На n карточках с двух сторон написаны числа от 1 до n по два раза каждое. Докажите, что карточки можно положить на стол так, чтобы сверху каждое из чисел было написано ровно один раз.

6.

Докажите утверждения, обратные сформулированным в задаче 2:

а)

Если в связном графе не более двух нечётных вершин, то в нём существует эйлеров путь.

б)

Если в связном графе степени всех вершин чётны, то в нём существует эйлеров цикл.

7.

На планете «Cube», имеющей форму куба, города расположены в вершинах куба и в серединах граней. Любые два города, расположенные на одном ребре, соединены дорогой. Также города, расположенные в серединах граней, соединены с вершинами. Космонавт хочет совершить путешествие по этой планете, пройдя по каждой из её дорог ровно один раз. Сможет ли он это сделать?

8.

На плоскости нарисованы несколько окружностей, образующих связную фигуру. Докажите, что её можно нарисовать, не отрывая карандаша от бумаги и проводя каждую линию один раз.

9.

Может ли ладья обойти шахматную доску, сделав каждый из возможных ходов ровно один раз? (Например, должны быть сделаны ходы: a1-a2, a1-a3, …, a1-a8, a1-b1, a1-c1, …, a1-h1 и т. д. для остальных клеток.)

10.

В некоторой стране из каждого города выходит по три железные дороги. Две компании хотят их все приватизировать. Антимонопольный комитет требует, чтобы из каждого города выходили дороги обеих компаний. Докажите, что компании могут договориться так, чтобы требование антимонопольного комитета было выполнено.