МАЛЫЙ МЕХМАТ МГУ

Кружок 6 класса
Руководитель Елена Анатольевна Чернышева
2005/2006 учебный год
2005/2006 учебный год
Математическая регата (4.02.2006)
Блок 1 (10 мин) (каждая задача — 6 баллов)
- 1-1.
-
Вычислите значение произведения: 77×9…9 (всего 2006 девяток).
Ответ. 76×9…923 (всего 2004 девятки)Решение. 77×9…9=77×(10…0 − 1)=770…0 − 77=769…923
- 1-2.
-
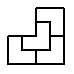
Разрежьте изображённую на рисунке фигуру четыре равные части.
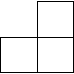
- 1-3.
-
Из спичек выложено равенство I/II − I/III = I/V. Переместите одну спичку так, чтобы равенство стало верным.
Решение. I/II + I/III = I/VI
Блок 2 (15 мин) (каждая задача — 7 баллов)
- 2-1.
-
Катя на выполнение домашнего задания тратит на 10% больше времени, чем Лена, а Маша тратит на 10% меньше времени, чем Катя. Кто из девочек быстрее всего делает домашнее задание?
Ответ. МашаРешение. Пусть Лена тратит на домашнее задание х времени, тогда Катя тратит 110% от х, то есть 1,1х, а Маша тратит 90% от времени Кати, то есть 90% от 1,1х, что составляет 0,9·1,1х=0,99х. Значит, быстрее всего домашнее задание делает Маша.
- 2-2.
-
Поставьте на шахматную доску как можно больше слонов, чтобы они не били друг друга.
Решение.
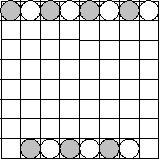
Рассмотрим диагонали, идущие справа налево сверху вниз. Всего на доске 8 таких диагоналей одного цвета, но при этом в противоположные угловые клетки нельзя поставить слонов, поэтому можно разместить не более 7 слонов одного цвета. - 2-3.
-
Средний рост восьми баскетболистов равен 195 см. Какое наибольшее количество из этих игроков может быть ниже, чем 191 см?
Ответ. СемьРешение. Если все восемь игроков ниже 191 см, то их средний рост меньше 191 см. Семь же игроков могут быть ниже, например, если один баскетболист имеет рост 230 см, а рост остальных — 190 см, то (230 + 190·7):8=195.
Блок 3 (15 мин) (каждая задача — 7 баллов)
- 3-1.
-
Температуру можно измерять в градусах Цельсия и Фаренгейта. Известно, что вода замерзает при 0° С, что соответствует 32° F, а кипит при 100° С или при 212° F. Сейчас на улице 5 градусов мороза по Цельсию. Какова температура по Фаренгейту?
Ответ. 23° FРешение. Из условия следует, что 100° С = 180° F, то есть, 1° С = 1,8° F. Поэтому, 5 градусам мороза по Цельсию соответствуют: 32° F – 5·1,8° F = 23° F.
- 3-2.
-
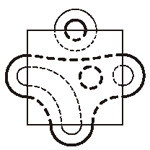
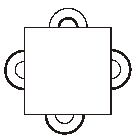
На столе лежат шесть непересекающихся контуров из проволоки, частично накрытые листом бумаги (см. рис.). Известно, что три контура сделаны из медной проволоки (она потолще), а три — из тонкой алюминиевой, причем один из контуров закрыт полностью, а пять других частично видны. Какой контур закрыт полностью, алюминиевый или медный? Свой ответ достаточно проиллюстрировать рисунком, показывающим расположение всех шести контуров.
- 3-3.
-
Найдите наименьшее составное число, которое не делится ни на одно из натуральных чисел от двух до десяти.
Ответ. 121Решение. Любое составное число является произведением не менее чем двух простых множителей. Из условия задачи следует, что каждый из этих множителей не может быть меньше, чем 11. Значит, искомое число не меньше, чем 11² = 121, а это число удовлетворяет условию.
Блок 4 (20 мин) (каждая задача — 8 баллов)
- 4-1.
-
Вася задумал число и прибавил к этому числу его сумму цифр. Петя также задумал число и тоже прибавил к нему его сумму цифр. В результате сложения у Васи и Пети получились одинаковые числа. Верно ли, что они задумывали одинаковые числа?
Ответ. Нет, неверноРешение. Например, если Вася задумал число 91, а Петя — число 100, то оба получили сумму 101.
- 4-2.
-
На плоскости расположены пять точек A, B, C, D и E так, что AC = 5 см, AE = 4 см; BC = 14 см, BD = 2 см, DE = 3 см. Найдите расстояние между серединами отрезков AB и CD.
Ответ. 3,5 смРешение.
Так как BD + DE + EA + AC = BC, то точки A, D и E лежат на отрезке BC так, как это показано на рис. Тогда AB = 9 см; CD = 12 см.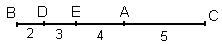
Искомое расстояние можно, например, вычислить так: середина отрезка AB удалена от точки B на половину длины AB, то есть, на 4,5 см. Середина отрезка CD удалена от точки C на половину длины CD, то есть, на 6 см. Следовательно, расстояние между серединами отрезков AB и CD равно14 – 4,5 – 6 = 3,5. - 4-3.
-
В вершинах треугольника записаны числа 1, 2 и 3. Затем каждое из чисел одновременно заменили на сумму двух соседних. Эту операцию проделали еще некоторое количество раз. Могла ли сумма получившихся в итоге трех чисел оказаться равной 3000000?
Решение. Пусть в какой-то момент в вершинах записаны числа а, b и с. Тогда после указанной операции вместо них будут записаны числа b + c, c + a и a + b. Так как (b + c) + (c + a) + (a + b) = 2(a + b + c), то после каждой операции сумма трёх записанных чисел удваивается. Сумма исходных чисел не делится на 5, поэтому и сумма чисел, полученных после любого количества операций, на 5 делиться не может.
Результаты регаты
| Команда | 1-1 | 1-2 | 1-3 | 2-1 | 2-2 | 2-3 | 3-1 | 3-2 | 3-3 | 4-1 | 4-2 | 4-3 | Σ |
| Happy End | 2 | 6 | 6 | 0 | 7 | 7 | 7 | 5 | 7 | 8 | 4 | 1 | 60 |
| Рваные шарики | 4 | 5 | 6 | 5 | 7 | 7 | 0 | 7 | 3 | 8 | 2 | 1 | 55 |
| МММФ-6 | - | 6 | 6 | 7 | 7 | 6 | 0 | 0 | 7 | 8 | - | 0 | 47 |
| Жираф! | 0 | 5 | 6 | 5 | 7 | 6 | 7 | 0 | 7 | 0 | 3 | 0 | 46 |
| Без названия | 2 | 6 | 6 | 7 | 7 | 6 | 1 | 7 | 3 | 0 | - | 0 | 45 |
Списки команд
|
|
| |||||||||||||||
|
|