МАЛЫЙ МЕХМАТ МГУ

Кружок 6 класса

Занятие 2 . Винегрет (15.10.2005)

1.

У императора украли перец. Как известно, те, кто крадёт перец, всегда лгут. Пресс-секретарь заявил, что знает, кто украл перец. Виновен ли он?

Ответ Решение

Ответ. Нет

Решение. Если он виновен, то знает, кто украл перец, значит, он говорит правду. Но если он виновен, он лжец. Предположив виновность пресс-секретаря, получили противоречие. Значит, он невиновен.

2.

У Вовочки живут девять котят, любителей сладкого. Однажды один из них слопал торт, и никто не сознался. Вовочка придумал взвесить их на чашечных весах без гирек. Все голодные котята весят одинаково. Может ли Вовочка найти сладкоежку за два взвешивания?

Ответ Решение

Ответ. Да, может.

Решение. Сажаем на чаши весов по три котёнка. Если чаши весов уравновешены, то сладкоежка — среди оставшихся, в противном случае он на более тяжёлой чаше. Из трёх «подозрительных» котят выбираем двух и сажаем по одному на чаши весов. Либо кто-то из них тяжелее, либо сладкоежка — третий.

3.

Крестьянину нужно переправить через реку двух волков, козу, капусту и собаку. Но волка нельзя оставлять без присмотра ни с козой, ни с собакой, собака в ссоре с козой, а коза неравнодушна к капусте. А лодка такова, что в ней может поместиться только крестьянин, а с ним — не более двух животных или одно животное и капуста. Как быть?

Решение

Решение. Крестьянин может сначала перевезти козу и собаку, потом вместе с козой вернуться за капустой, снова вместе с козой вернуться, оставить козу и перевезти волков, вместе с собакой вернуться за козой и отвезти козу и собаку.

4.

Два котёнка и два щенка съели килограмм сосисок. Рыжий котёнок съел больше всех, а серый — не меньше всех. Может ли быть так, что щенки съели больше сосисок, чем котята?

Ответ Решение

Ответ. Нет, такого быть не может.

Решение. Серый котёнок съел не меньше всех, значит, существует кто-то, кто съел не больше его, и это не рыжий котёнок. Значит, один из щенков съел не больше серого котёнка, а второй — меньше рыжего. Значит, щенки съели меньше сосисок, чем котята.

5.

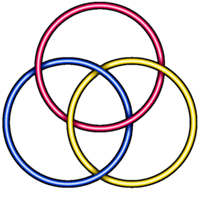
Можно ли из трёх бумажных колец сделать такую цепочку, чтобы при разрезании одного любого звена цепочка распалась на три отдельные части?

Ответ Решение

Ответ. Да, можно.

Решение. Эту конфигурацию называют «кольца Борромео». Когда-то давным давно в Италии был знатный род Борромео и на их гербе была ровно такая конфигурация. Один из них — Карло Борромео — даже причислен к лику святых.

6.

Два поезда, оба длиной по 50 м, движутся навстречу друг другу с одинаковой скоростью 45 км/ч. Сколько времени пройдёт от момента, когда встретятся машинисты, до момента, когда встретятся проводники последних вагонов?

Ответ Решение

Ответ. 4 секунды.

Решение. В момент встречи машинистов расстояние между проводниками будет 100 м. Так как каждый поезд движется со скоростью 45 км/ч, то проводники сближаются со скоростью 90 км/ч или 25 м/с. Искомое время равно 100:25=4 секунды.

7.

Горят две свечи неодинаковой длины и толщины. Более длинная полностью сгорает за три с половиной часа, а короткая — за пять часов. Через два часа одновременного горения их длины оказались равными. Во сколько раз одна свеча была первоначально короче другой?

Ответ Решение

Ответ. В 1,4 раза.

Решение. Если короткая свеча сгорает за пять часов, то за один час сгорает ¹/₅ короткой свечи. Аналогично за один час сгорает 1:3,5=²/₇ длинной свечи. Через два часа осталось ³/₅ короткой свечи и ³/₇ длинной свечи, причём эти огарки одинаковой высоты. Получаем, что пятая часть короткой свечи равна седьмой части длинной свечи, то есть одна свеча короче другой в ⁷/₅ раза.

8.

Можно ли разрезать квадрат на двенадцать квадратов?

Ответ Решение

Ответ. Да, можно.

Решение.