МАЛЫЙ МЕХМАТ МГУ

Кружок 6 класса
Руководитель Елена Анатольевна Чернышева
2005/2006 учебный год
2005/2006 учебный год
Занятие 11. Кто больше?(28.01.2006)
- 1.
- В примере 60 + 40:4 − 2 расставьте скобки так, чтобы получился а) как можно меньший; б) как можно больший результат.
- 2.
-
Разместите в квадрате 10×10 как можно больше фигур-скобок,
изображённых на рисунке.
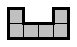
Ответ. Наибольшее число скобок — 16. - 3.
- Используя известные математические символы, получите число 2006 с помощью как можно меньшего количества единиц.
- 4.
-
Найдите как можно меньшее четырехзначное число СЕЕМ, для которого
существует решение ребуса МЫ + РОЖЬ = СЕЕМ. (Одинаковым буквам соответствуют одинаковые цифры, разным — разные.)
Ответ. 2003Решение. Поскольку C > P, C > 1. Так как мы ищем наименьшее число, попробуем взять P=1, C=2 и E=0. Тогда M > 2. Случай CEEM=2003 возможен: 35 + 1968=2003 или 38 + 1965=2003.
- 5.
-
Художник-авангардист Змий Клеточкин покрасил несколько клеток
доски размером 7×7, соблюдая правило: каждая следующая
закрашиваемая клетка должна соседствовать по стороне с предыдущей
закрашенной клеткой, но не должна — ни с одной другой ранее
закрашенной клеткой. Покрасьте как можно больше клеток доски таким
способом.
Ответ. Можно покрасить 33 клеточки.
- 6.
-
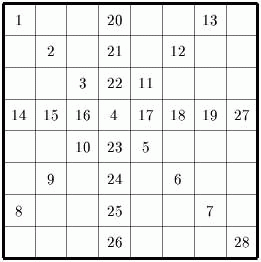
Числа на клетчатой доске 8×8 можно ставить следующим
образом. Сначала ставится число 1 в любую клетку. Потом ставится
число 2 таким образом, чтобы фигура из клеток 1 и 2 имела ось
симметрии. Затем ставится число 3 так, чтобы фигура из клеток 1, 2 и
3 имела ось симметрии. И так далее. Поставьте как можно больше
чисел.
Ответ. Можно поставить 28 чисел.
- 7.
-
В одной из вершин куба сидит заяц, но охотникам он не виден. Три
охотника стреляют залпом, при этом они «поражают» любые три
вершины куба. Если они не попали в зайца, то до следующего залпа
заяц перебегает в одну из трёх соседних (по ребру) вершин. Укажите,
как стрелять охотникам, чтобы обязательно попасть в зайца за как
можно меньшее число залпов.
Ответ. Минимальное число залпов — четыре. Охотники обязательно попадут в зайца, сделав следующие залпы: (CFH), (BDE), (DEG), (ACF). (Порядок залпов важен!)Решение.
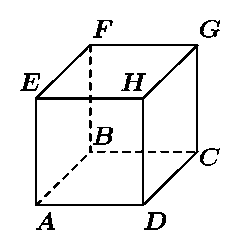
Покрасим вершины A, C, F и H в чёрный цвет, а остальные вершины — в белый. Заметим, что любые две соседние вершины будут покрашены в разные цвета. Значит, после каждого залпа заяц перебегает в вершину другого цвета. Сделаем первый залп по вершинам C, F и H. Если заяц находился в чёрной вершине, то либо охотники сразу попали в него, либо заяц находился в вершине A. В последнем случае после залпа заяц перебежит в одну из трех соседних вершин, и залп (BDE) обязательно достигнет цели. Если заяц находился в белой вершине, то после двух выстрелов он снова окажется в белой вершине. Рассуждая аналогично предыдущему случаю, убеждаемся, что залпы (DEG), а потом (ACF) обязательно поразят зайца.
Кто больше:
| Фамилия | Имя | Примеры | Доказательства | СУММА |
| Заводов | Алексей | 15 | 40 | 55 |
| Решетников | Иван | 10 | 30 | 40 |
| Подольский | Александр | 18 | 20 | 38 |
| Салахетдинов | Руслан | 17 | 20 | 37 |
| Жуков | Георгий | 16 | 20 | 36 |
| Журихина | Анастасия | 11 | 20 | 31 |
| Кондаков | Даниил | 10 | 20 | 30 |
| Ландо | Андрей | 6 | 20 | 26 |
| Какурин | Даниил | 5 | 20 | 25 |
| Коротов | Денис | 2 | 20 | 22 |
| Горбач | Михаил | 9 | 10 | 19 |
| Аржакова | Елизавета | 8 | 10 | 18 |
| Афанасьева | Анастасия | 8 | 10 | 18 |
| Дорофеев | Евгений | 8 | 10 | 18 |
| Петрин | Александр | 8 | 10 | 18 |
| Гребеник | Николай | 6 | 10 | 16 |
| Изотова | Ирина | 6 | 10 | 16 |
| Кириллов | Павел | 6 | 10 | 16 |
| Столяров | Арсений | 16 | 0 | 16 |
| Левин | Александр | 5 | 10 | 15 |
| Орехова | Алена | 5 | 10 | 15 |
| Сущенко | Павел | 8 | 0 | 8 |
| Николаев | Андрей | 5 | 0 | 5 |
| Довжик | Виктор | 3 | 0 | 3 |
| Зыбинов | Никита | 3 | 0 | 3 |
| Гончаренко | Иван | 0 | 0 | 0 |
| Довжик | Сергей | 0 | 0 | 0 |