МАЛЫЙ МЕХМАТ МГУ

Кружок 6 класса

Занятие 12. Графы и графини (11.02.2006)

1.

Гарри Поттер умеет превращать жабу в принцессу, гриб в жабу и грушу, грушу в яблоко, огрызок от яблока в котёнка и ёжика, котёнка в грушу или яблоко, ёжика в грушу, а яблоко — только в огрызок. Сейчас у него есть яблоко. Сможет ли он превратить его в принцессу?

Ответ Решение

Ответ. Нет, не сможет.

Решение. Так как принцессу можно получить только из жабы, а жабу только из гриба, то если бы это было возможно, Гарри Поттеру нужно было бы получить гриб. Но ничто из перечисленного в условии задачи в гриб превратить нельзя.

2.

На День рождения к Андрею пришли Вася, Глеб, Даша, Митя, Петя, Соня и Тимур. Покажите, как восьмерых ребят можно рассадить за круглый стол, чтобы у любых двух, сидящих рядом, в именах встречались одинаковые буквы.

Ответ

Ответ. Андрей — Глеб — Петя — Тимур — Митя — Соня — Вася — Даша — Андрей.

3.

В одном государстве из каждого города выходит по три дороги. Может ли быть в этом государстве а) 100 дорог? б) 100 городов?

Ответ Решение

Ответ. а) Нет, не может. б) Может.

Решение.
а) Пусть в этом государстве g городов. Построим остановки на концах каждой дороги. Посчитаем количество построенных остановок. С одной стороны, количество остановок равно 3g, так как из каждого из городов выходит по три дороги. А с другой стороны, это количество равно удвоенному числу дорог, так как на каждой дороге построено две остановки. Таким образом, если бы в этой стране было 100 дорог, то выполнялось бы равенство: 3g=200. Но это равенство выполняться не может, так как 3g делится на 3, 200 — нет.
б) Разобьём все города на четвёрки и соединим дорогой любые два города, которые входят в одну четвёрку. А города из разных четвёрок соединять не будем. Нетрудно убедиться в том, что такая ситуация удовлетворяет условию задачи.

4.

Пешеход обошёл все улицы одного города, пройдя каждую ровно два раза, но не смог обойти их, пройдя каждую лишь раз. Могло ли такое быть?

Ответ Решение

Ответ. Такое могло быть

Решение. Например, в таком случае (см. рис.):

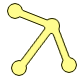
Нетрудно убедиться в том, что пешеход мог обойти все улицы, пройдя по каждой дважды, если бы начал своё путешествие с «центральной» площади — от которой отходит три улицы. Докажем, что он не мог обойти каждую улицу ровно один раз. Он не мог начать обход с «центральной» площади — в этом случае он после первой же улицы оказывается в тупике. А если бы он начал обход с любой из остальных площадей, то, пройдя первую улицу, оказался бы на «центральной» площади, а после неё — опять в тупике. По третьей улице ему пройти не удастся.

5.

Чипполино устроился садовником к графине Вишне. Графиня установила для него повременную форму оплаты труда, при которой тарифная ставка в час составляла 3 монеты. Чипполино работал несколько дней по 6 часов, а несколько дней — по 8 часов, и заработал 78 монет. Сколько дней он мог работать по 6 часов?

Ответ Решение

Ответ. 3 дня.

Решение. Так как в час Чипполино зарабатывал по 3 монеты и всего заработал их 78, то он отработал 26 часов. Пусть a — количество дней, в которые Чипполино работал по 6 часов, b — количество дней, в которые он работал по 8 часов. Тогда 6a + 8b = 26. Из этого следует, что 3a + 4b = 13. Значит, выражение 4b может быть равно 0, 4, 8 или 12, то есть b равно 0, 1, 2 или 3. Рассмотрим все возможные случаи для значения b: b = 0 ⇒ 3a + 4 · 0 = 13 ⇒ 3a = 13
b = 1 ⇒ 3a + 4 · 1 = 13 ⇒ 3a = 9
b = 2 ⇒ 3a + 4 · 2 = 13 ⇒ 3a = 5
b = 3 ⇒ 3a + 4 · 3 = 13 ⇒ 3a = 1 Только во втором случае a принимает целое значение, равное 3. Таким образом, Чипполино мог работать по 6 часов 3 дня.

6.

Вдоль границ каждой клетки шахматной доски положили спички. Необходимо убрать несколько спичек, чтобы ладья могла добраться с любого поля на любое, не перепрыгивая через спички. На рисунке убрано 70 спичек. Можно ли обойтись меньшим количеством? Какое минимальное количество спичек надо убрать?

Ответ Решение

Ответ. Можно обойтись 63 спичками.

Решение. Для этого нужно убрать все горизонтальные спички, кроме тех, которые лежат по краям доски, и вертикальные спички в нижней строке, кроме тех, которые лежат по краям доски. Покажем, что меньшим числом спичек обойтись нельзя. Поставим ладью в одну из клеток доски: пусть она обходит всё поле. Положим все спички обратно и будем убирать их только в тот момент, когда они мешают ладье. Ладья должна побывать на 63 клетках. В тот момент, когда ладья ходит на какую-то клетку в первый раз, убираем мешающую ей спичку. В начальный момент все 63 клетки от ладьи закрыты. Когда мы убрали одну спичку, 62 клетки остались для ладьи закрыты. Чтобы попасть на новую клетку, нужно снова убрать спичку. Убрав одну спичку, мы к доступному ладье пространству присоединим одну клетку. В каждый момент времени ладья может свободно перемещаться по «старым» клеткам, но, чтобы попасть на новую, нужно убрать спичку. Получается, чтобы попасть во все 63 клетки, нужно убрать минимум 63 спички.

7.

Верно ли, что в вашем классе найдутся два школьника, у которых одинаковое число друзей среди учащихся класса? Верно ли это для любого класса?

Ответ Решение

Ответ. Это верно для любого класса.

Решение. Пусть в классе n учеников. У каждого из них может быть от 0 до n − 1 друзей — один из n возможных вариантов (количество целых чисел от 0 до n − 1 равно n). Если бы в классе у любых двух детей было бы разное количество друзей, то у кого-то было бы 0 друзей, у кого-то был бы 1 друг, …, у кого-то был бы n − 1 друг (так как количество человек равно количеству вариантов для числа друзей). Но в классе не может быть одновременно человек, у которого 0 друзей, и человек, у которого n − 1 друг, так как первый не дружит ни с кем, а второй дружит со всеми.

8.

Докажите, что среди любых шести человек всегда найдутся либо трое попарно знакомых, либо трое попарно незнакомых.

Решение

Решение.
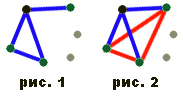
Поставим шесть точек, соответствующие шести людям. Если люди знакомы между собой, соединим соответствующие точки красным отрезком, если не знакомы, то синим. Тогда, если на нашем рисунке есть красный треугольник, это означает, что существует три попарно знакомых между собой человека, а если есть синий треугольник, то существует три попарно незнакомых между собой человека.
Рассмотрим любую из шести точек. Из неё выходит пять отрезков. Из пяти отрезков есть по крайней мере три одного цвета. Предположим, есть три синих отрезка (случай, когда есть три красных отрезка, рассматривается аналогично.)
Если какие-то два конца этих отрезков соединены между собой синим, то есть синий треугольник (см. первый рис.).
Если же все концы этих отрезков соединены между собой красным, то получается, что есть красный треугольник (см. второй рис.).