МАЛЫЙ МЕХМАТ МГУ

Кружок 6 класса
Руководитель Елена Анатольевна Чернышева
2005/2006 учебный год
2005/2006 учебный год
Занятие 17. Плоские графы (18.03.2006)
Граф, который можно нарисовать так, чтобы его рёбра не пересекались (нигде, кроме вершин) называется плоским. Будем говорить, что плоский граф правильно нарисован, если его рёбра на рисунке не пересекаются. Заметим, что плоский правильно нарисованный граф разбивает плоскость на несколько частей.
- 1.
-
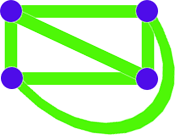
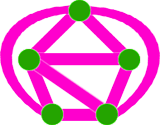
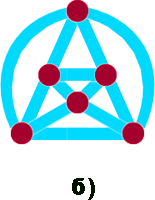
Являются ли плоскими графы, изображённые на рисунке?

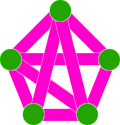
Ответ. Являются. - 2.
-
а) Нарисуйте правильно плоский граф, вершины которого соответствуют вершинам куба, а рёбра — рёбрам куба.
б) Нарисуйте плоский граф для октаэдра (многогранника, у которого 6 вершин, 8 граней и 12 рёбер). Для любого ли правильного или полуправильного многогранника можно нарисовать плоский граф?Решение. Плоский граф можно нарисовать для любого многогранника. Для этого нужно достаточно сильно «растянуть» рёбра одной из его граней так, чтобы площадь этой грани стала больше, чем сумма площадей всех остальных. Затем нужно спроецировать в плоскость этой «большой» грани все вершины многогранника вместе с рёбрами (кроме вершин самой этой грани, так как они и так в ней лежат), изменив при этом конфигурацию некоторых рёбер, если это нужно.
Понятно, что приведённое доказательство не является строгим — мы просто хотели подсказать красивую идею, которая помогает понять, как это сделать. Строгое доказательство для произвольного многогранника требует ещё некоторых не совсем простых рассуждений. Но нетрудно убедиться в том, что для правильного или полуправильного многогранника утверждение задачи верно.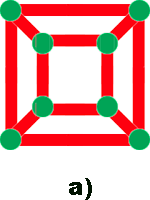
Для плоского правильно нарисованного графа введём обозначения: В — количество вершин в нём, Р — количество рёбер, Г — количество частей, на которые он разбивает плоскость (количество граней).
- 3.
-
Докажите, что В — Р + Г = 2 для произвольного дерева.
Решение. Как известно, в дереве количество вершин на единицу больше количества рёбер, то есть, В — Р = 1. Кроме того, так как в дереве нет циклов, то количество частей (граней), на которые оно разбивает плоскость, равно единице: эта грань вся плоскость. То есть Г = 1. Тогда получается, что для любого дерева выполняется соотношение В — Р + Г = 1 + 1 = 2, что и требовалось доказать.
- 4.
-
Докажите, что в любом связном графе можно удалить некоторое количество рёбер так, что он станет деревом.
Решение. Если связный граф не является деревом, то это означает, что в нём есть циклы (дерево по определению — это связный граф без циклов). Возьмём любой из циклов и удалим в нём произвольное ребро. Понятно, что граф останется связным. Если после удаления одного ребра циклов не осталось, то исходный граф стал деревом — мы получили то, что нужно. Если циклы остались, то опять берём любой из них и удаляем в нём произвольное ребро. В графе конечное число циклов (так как рёбер конечное число), поэтому рано или поздно с помощью проведения указанной операции мы добьёмся того, что циклов не останется и граф превратится в дерево.
- 5.
-
Докажите, что В — Р + Г = 2 для плоского правильного нарисованного графа. (Формула Эйлера.)
Решение. Если граф является деревом, то утверждение для него уже доказано в задаче №3.
Если же граф имеет циклы, то повторим рассуждение из решения задачи №3: будем удалять в этом графе по одному ребру до тех пор, пока все циклы не исчезнут. При удалении очередного ребра разрушается один цикл, поэтому количество граней уменьшается на 1. Количество вершин не изменяется, количество рёбер тоже уменьшается на 1. Получается, что при удалении каждого ребра значение выражения В — Р + Г не изменяется, так как и Р, и Г уменьшаются на 1, но перед Р стоит знак «минус», а перед Г — «плюс». Когда в графе не останется циклов (то есть он станет деревом), то, как мы доказали ранее, значение выражения В — Р + Г будет равно 2, а так как при выполнении указанных операций оно не менялось, то и изначально оно было равно 2. - 6.
-
В стране Озёрная 7 озёр, соединённых между собой 10 каналами, причём от любого озера можно доплыть до любого другого. Сколько в этой стране островов?
Ответ. 4 острова.Решение. Рассмотрим граф, в котором вершины соответствуют островам, а рёбра — каналам. Понятно, что полученный граф будет плоским и связным, значит, для него выполняется формула Эйлера: В — Р + Г = 2. Для нашего графа В = 7, Р = 10. Подставляя в формулу, получаем 7 — 10 + Г = 2. Отсюда следует, что Г = 5, то есть, рёбра графа разбивают плоскость на 5 частей. Островам соответствуют все грани, кроме внешней (она бесконечно большая во все стороны и острову соответствовать не может), значит, их 4.
- 7.
-
Задача про футбольный мяч. В многограннике чёрные грани — правильные пятиугольники, а белые — правильные шестиугольники. В каждой вершине сходится по три грани. Сколько в этом многограннике чёрных граней?
Ответ. 12 чёрных граней.Решение. Так как любому многограннику соответствует плоский связный граф (см. решение задачи №2), то для многогранников также верна формула Эйлера: В — Р + Г = 2.
Будем считать, что поверхность данного многогранника состоит из П пятиугольников и Ш шестиугольников. То есть Г = П + Ш.
Подсчитаем для каждой грани, сколько вершин многогранника ей принадлежит, и сложим полученные числа. Каждому пятиугольнику принадлежит 5 вершин, а каждому шестиугольнику 6. Так как пятиугольников П, шестиугольников Ш, то в итоге после суммирования получится число 5П + 6Ш. При этом в полученной сумме каждая вершина посчитана по 3 раза, так как к каждой вершине прилегает 3 грани. Поэтому выполняется соотношение:5П + 6Ш = 3Вили
Теперь получим соотношение для рёбер. У каждого пятиугольника 5 сторон, а у шестиугольника — шесть, поэтому если для каждой грани подсчитать количество прилегающих к ней рёбер, а затем полученные числа сложить, то каждое ребро будет посчитано ровно два раза, так как любое из них прилегает ровно к двум сторонам. Тогда выполняется соотношение:В = 5П + 6Ш 3 5П + 6Ш = 2Рили
Подставим полученные выражения в формулу Эйлера.Р = 5П + 6Ш 2
Откуда5П + 6Ш - 5П + 6Ш + (П + Ш) = 2 3 2 10П + 12Ш - 15П – 18Ш + 6П + 6Ш = 12П = 12 - 8.
-
В квадрате отметили 20 точек и соединили их непересекающимися отрезками друг с другом и вершинами квадрата так, что квадрат разбился на треугольники. Сколько получилось треугольников?
Ответ. 42 треугольника.Указание. Рассмотрите граф, в котором 24 вершины и все грани, кроме внешней, треугольные.
- 9.
- Каждое ребро полного графа с 11 вершинами покрашено в один из двух цветов: красный или синий. Докажите, что либо «красный», либо «синий» граф (либо и тот, и другой) не является плоским.