МАЛЫЙ МЕХМАТ МГУ

Кружок 7 класса

Занятие 2 (26 октября 2015 года)

1.

а)

В комнате лежали 101 коробка, в каждой по 100 конфет. Ванечка взял из первой коробки 0 конфет, из второй — 1, из третьей — 2, и так далее, а после того, как забрал все 100 конфет из сто первой коробки, он вскочил и убежал с хихиканьем. Потом пришёл Григорий и забрал всё остальное. Кому из них досталось больше?

б)

Сколько всего было конфет? Сколько досталось Ванечке?

2.

а)

В первый день дракон съел 50 рыцарей. От полученных во время обеда ран он немного ослабел, и поэтому во второй день съел только 49 рыцарей. В третий — 48, в четвёртый — 47, и так далее, пока в последний день он не скончался после поедания всего одного рыцаря. Сколько дней дракон ел рыцарей, и скольких он съел?

б)

Каким бы был ответ на этот вопрос, если бы дракон скончался раньше, в день, когда было съедено 23 рыцаря?

3.

а)

В ряд выстроились 20 эльфов. Оказалось, что каких двух из них не возьми, всегда в этой паре будет хотя бы один на самом деле — тролль. Сколько троллей может скрываться среди этих эльфов?

б)

Оказалось, что из любых трёх «эльфов», стоящих подряд в этом ряду, хотя бы два страдают от избыточного веса. Сколько толстых «эльфов» может быть в ряду?

4.

а)

Сколько ладей можно поставить на доску 9×9 так, чтобы они не били друг друга? (Ладья бьёт по горизонтали и по вертикали на любое количество клеток.)

б)

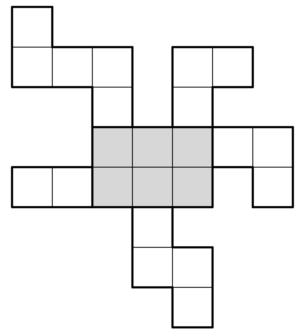
Сколько ладей можно поставить на осьминожку справа так, чтобы они не били друг друга?

5.

Проверяя, что кусок материи имеет форму квадрата, швея перегибает его по каждой диагонали и убеждается, что края каждый раз совпадают. Достаточна ли такая проверка?

6.

Когда Петя разбил свою копилку, в ней было меньше 100 монет. Петя разложил их на кучки по 2 монеты, но одна осталась лишней. Тогда Петя разложил их на кучки по 3 монеты, и снова одна осталась лишней. То же произошло, когда Петя разложил их на кучки по 4 монеты, и когда — по 5. Сколько монет было в копилке?

7.

а)

Несколько ящиков вместе весят 10 т, причем каждый из них весит не более 1 т. Докажите, что пяти трехтонных грузовиков наверняка хватит, чтобы увезти этот груз.

б)

Могут ли ящики быть такие, что четырёх грузовиков не хватит?

8.

Как положить на стол несколько одинаковых монет так, чтобы каждая касалась ровно трёх других? (Все монеты должны лежать на столе, нельзя класть одну на другую, ставить на ребро и т. д.)