МАЛЫЙ МЕХМАТ МГУ

Кружок 5 класса

Занятие 21 (5 апреля 2014 года)

1.

Разрежьте фигуры, изображённые на рисунках, на равные части так, чтобы в каждой части был ровно 1 кружок.

2.

Антоше подарили весы, и он начал взвешивать игрушки. Машину уравновесили мяч и 2 кубика, а машину с кубиком уравновесили 2 мяча. Сколько кубиков уравновесят машину?

3.

а)

Сегодня суббота. Какой день недели будет через 2014 дней? А какой день недели был 2014 дней назад?

б)

На доске записано число 61. Каждую минуту число стирают с доски и записывают на это место произведение его цифр, увеличенное на 13. Например, через минуту на доске запишут значение выражения 6· 1 + 13, то есть 19. Какое число будет на доске через 100 минут?

4.

В дремучем лесу вот уже более сотни лет живёт Волшебная ёлка. Известно, что каждое утро на ней вырастает 100 иголок и каждая иголка живёт ровно 4 года, а затем отмирает. Сколько же иголок было на Волшебной ёлке сегодня ровно в полдень?

5.

В одной урне лежат два белых шара, в другой два чёрных, в третьей — один белый и один чёрный. На каждой урне висела табличка, указывающая её содержимое: ББ, ЧЧ, БЧ. Некто перевесил таблички так, что теперь каждая табличка указывает содержимое урны неправильно. Разрешается вынуть шар из любой урны, не заглядывая в неё. Какое наименьшее число извлечений потребуется, чтобы определить состав всех трёх урн?

6.

Закрасьте несколько клеток так, чтобы каждая клетка граничила по стороне ровно с двумя закрашенными

а)

на поверхности куба 2×2×2;

б)

на доске 8×8.

Дополнительные задачи

7.

Расположите по кругу числа от 1 до 10 так, чтобы для любых двух соседних чисел их сумма была бы равна сумме двух чисел, им противоположных (симметричных относительно центра окружности).

8.

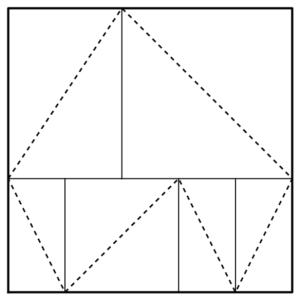
Малый и Большой острова имеют прямоугольную форму и разделены на прямоугольные графства. В каждом графстве проложена дорога по одной из диагоналей. На каждом острове эти дороги образуют замкнутый путь, который ни через какую точку не проходит дважды. На рисунке изображено, как устроен Малый остров, где всего 6 графств. Нарисуйте, как может быть устроен Большой остров, если на нём нечётное число графств.

9.

Четыре кузнечика сидят в вершинах квадрата. Каждую минуту один из них прыгает в точку, симметричную ему относительно другого кузнечика. Докажите, что три кузнечика никогда не смогут оказаться на одной прямой, параллельной стороне квадрата.