МАЛЫЙ МЕХМАТ МГУ

Кружок 5 класса

Занятие 12 (7 декабря 2013 года)

1.

В коробке лежат синие, красные и зелёные карандаши. Всего 20 штук. Синих в 3 раза больше, чем зелёных, красных меньше, чем синих. Сколько может быть в этой коробке красных карандашей?

2.

За сколько ходов можно собрать пазл из 2000 элементов, если за один ход считать соединение двух кусков (независимо от того, из скольких элементов они уже состоят)?

3.

На одном заводе работают три друга: слесарь, токарь и сварщик. Их фамилии: Борисов, Иванов и Семёнов. У слесаря нет ни братьев, ни сестёр; он самый младший из друзей. Семёнов старше токаря и женат на сестре Борисова. Назовите фамилии слесаря, токаря и сварщика.

4.

В 2 часа дня настенные часы били в течение 5 секунд, а в 4 часа дня — 11 секунд. Сколько секунд они будут бить в 6 часов? (Продолжительность всех ударов одинакова, продолжительность пауз между ударами тоже одинакова.)

5.

Незнайкин счёт в банке содержит 500 фертингов. Банк разрешает совершать операции только двух видов: снимать 300 фертингов или добавлять 198 фертингов. Какую максимальную сумму Незнайка может снять со счёта, если других денег у него нет?

6.

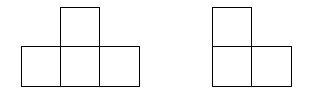
Пете и Коле выдали две одинаковые фигуры, вырезанные из клетчатой бумаги. Известно, что в каждой фигуре меньше чем 16 клеток. Петя разрезал свою фигуру на части из четырёх клеток, а Коля разрезал свою фигуру на уголки из трёх клеток (см. рисунок). Приведите пример фигуры, которую могли выдать мальчикам. Покажите, как эту фигуру разрезал на части Петя, и как её разрезал Коля.

Дополнительные задачи

7.

Первая слева цифра десятизначного числа равна числу единиц в записи этого числа, вторая — числу двоек, третья — числу троек, ..., девятая — числу девяток, десятая — числу нулей. Приведите пример такого числа.

8.

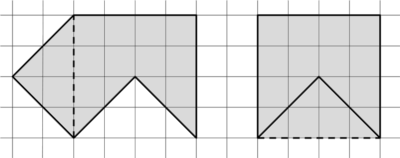
Серёжа придумал фигуру, которую легко разрезать на две части и сложить из них квадрат (см. рисунок). Покажите как по-другому разрезать эту фигуру на две части, из которых тоже можно сложить квадрат.

9.

Петя разрезал прямоугольный лист бумаги по прямой. Затем он разрезал по прямой один из двух кусков. Затем он проделал то же самое с одним из трёх получившихся кусков и так далее. Докажите, что после достаточного количества разрезаний обязательно можно будет выбрать среди получившихся кусков 100 многоугольников с одинаковым числом вершин (например, 100 треугольников или 100 четырёхугольников и т.д.).