МАЛЫЙ МЕХМАТ МГУ

Кружок 5 класса

Занятие 17 (1 марта 2014 года)

1.

В 13-этажном доме имеется лифт с четырьмя кнопками: «+9», «−9», «+7», «−7».

а)

Можно ли проехать с 4-го этажа на 9-ый?

б)

Незнайка вынужден подниматься домой по лестнице, поскольку на лифте с первого этажа до его этажа добраться невозможно. Более того, он вынужден подниматься пешком со своего этажа на 13-й, где живёт его друг Знайка. Сможете ли вы по этим данным определить, на каком этаже живёт Незнайка?

2.

Однажды, гуляя в лесу, Маша обнаружила полянку, вокруг которой росли сосны. Маша выяснила, что высота любых двух соседних сосен отличается ровно на 1 метр. Могло ли на полянке быть ровно а) 3; б) 4; в) 2013; г) 2014 сосен?

3.

Очень хитрый киоскёр получил для продажи несколько пачек конвертов по 100 конвертов в каждой. 10 конвертов он отсчитывает за 10 секунд. Оказалось, что 70 конвертов он отсчитывает быстрее, чем 40. Как? А за сколько секунд он может отсчитать 360 конвертов?

4.

Однажды в четверг после дождя между двумя жителями острова Рыцарей и лжецов Тимом и Томом произошёл следующий диалог. «Ты можешь сказать, что я рыцарь,» — гордо заявил Тим. «Ты можешь сказать, что я лжец,» — грустно ответил ему Том. Кем являются Тим и Том?

5.

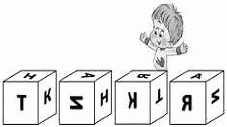
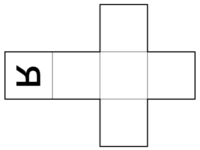
Ребёнок поставил четыре одинаковых кубика так, что буквы на сторонах кубиков, обращённых к нему, образуют его имя (см. рисунок). Нарисуйте, как расположены остальные буквы на данной развёртке кубика, и определите, как зовут ребёнка.

6.

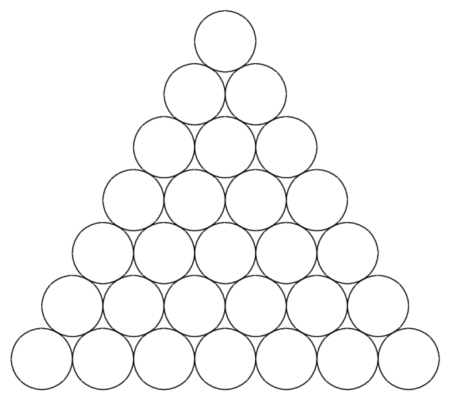
На столе в виде треугольника выложены 28 монет одинакового размера, но не все они имеют одинаковую массу. Известно, что суммарная масса любой тройки монет, которые попарно касаются друг друга, равна 10 г. Найдите суммарную массу всех 18 монет на границе треугольника.

Дополнительные задачи

7.

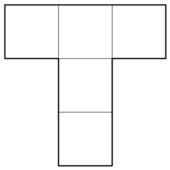
Нарисуйте фигуру, которую можно разрезать на четыре фигурки, изображённые слева, а можно --– на пять фигурок, изображённых справа. (Фигурки можно поворачивать.)

8.

В одной из вершин куба сидит заяц, но охотникам он не виден. Три охотника стреляют залпом, при этом они могут «поразить» любые три вершины куба. Если они не попадают в зайца, то до следующего залпа заяц перебегает в одну из трёх соседних (по ребру) вершин куба. Укажите, как стрелять охотникам, чтобы обязательно попасть в зайца за четыре залпа.

9.

В Пустоземье живут три племени: эльфы, гоблины и хоббиты. Эльф всегда говорит только правду, гоблин всегда лжёт, а хоббит через раз говорит то правду, то ложь. Однажды за круглым столом пировало несколько пустоземцев, и один из них сказал, указав на своего левого соседа: «Он — хоббит». Сосед сказал: «Мой правый сосед солгал». В точности ту же фразу затем повторил его левый сосед, потом её же произнёс следующий по кругу, и так они говорили «Мой правый сосед солгал» много-много кругов, да и сейчас ещё, возможно, говорят. Определите, из каких племён были пирующие, если известно, что за столом сидело а) девять; б) десять жителей Пустоземья.