МАЛЫЙ МЕХМАТ МГУ

Кружок 5 класса

Занятие 16 (22 февраля 2014 года)

1.

На батоне колбасы нарисованы тонкие поперечные кольца. Если разрезать по красным кольцам, получится 5 кусков, если по жёлтым — 7 кусков, а если по зелёным — 11 кусков. Сколько кусков колбасы получится, если разрезать по кольцам всех трёх цветов?

2.

Паучок, сидевший в вершине куба, отправился гулять по рёбрам. Каждую минуту он проползает ровно одно ребро и не задерживается в вершинах. Нарисуйте, в каких вершинах он может оказаться а) ровно через 2 минуты; б) через 3 минуты; в) через 10 минут.

3.

Пять футбольных команд провели турнир: каждая команда сыграла с каждой по разу. За победу начислялось 3 очка, за ничью — 1 очко, за проигрыш очков не давалось. Четыре команды набрали соответственно 1, 2, 5 и 7 очков. А сколько очков набрала оставшаяся команда?

4.

Лёша, Сеня и Ваня играют в настольный теннис, причём тот, кто не принимает участие в партии, в следующей играет с победителем предыдущей. В результате Лёша сыграл 10 партий, а Сеня — 21. Сколько партий сыграл Ваня?

5.

В Солнечном городе живут 25 коротышек. У каждого из них есть три воздушных шарика: красный, синий и жёлтый. Смогут ли они так поменяться шариками, чтобы у каждого все три шарика оказались одноцветными?

6.

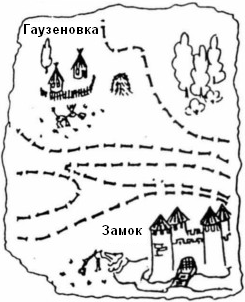
Давным-давно барон фон Мюнхгаузен обнёс свои владения забором и нарисовал его на карте. Забор был изображён замкнутой несамопересекающейся линией, внутри которой — владения барона. Барон забыл, входит ли в его владения деревня Гаузеновка. К сожалению, он смог найти лишь обрывок карты, на который попали его дом, деревня Гаузеновка и часть забора. Входит ли деревня во владения барона?

Дополнительные задачи

7.

Каждая грань куба поделена на 4 равных квадрата. Каждый квадрат покрашен в один из трёх цветов: синий, зелёный или оранжевый так, что квадраты, имеющие общую сторону, окрашены в разные цвета. Сколько при этом может получиться синих, зелёных и оранжевых квадратов?

8.

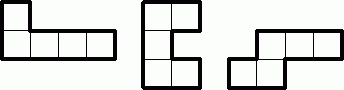
Нарисуйте, как из данных трёх фигурок, использовав каждую ровно один раз, сложить фигуру, имеющую ось симметрии.

9.

На острове Невезения с населением 24 человека правительство решило провести пять реформ. Каждой реформой недовольна ровно половина всех граждан. Гражданин выходит на митинг, если он недоволен более чем половиной всех реформ. Какое максимальное число людей правительство может ожидать на митинге?