МАЛЫЙ МЕХМАТ МГУ

Кружок 5 класса

Занятие 14 (8 февраля 2014 года)

1.

Настя сказала: «Позавчера мне было 10 лет, а в следующем году исполнится 13». Могло ли сказанное быть правдой?

2.

По шесту высотой 20 метров ползёт улитка. За день она поднимается на 3 метра вверх, а за ночь съезжает на 2 метра вниз. За сколько дней улитка доберётся до вершины шеста?

3.

На рисунке изображён прямоугольник, составленный из шести квадратов. Найдите сторону самого большого квадрата, если сторона самого маленького равна 1.

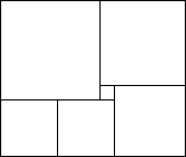
4.

Семь школьников участвуют в шахматном турнире по круговой системе (каждый играет с каждым ровно один раз). К началу обеденного перерыва оказалось, что Ваня сыграл шесть партий, Толя — пять, Лёша и Дима — по три, Семён и Илья — по две, Женя — одну. С кем успел сыграть Лёша?

5.

В ящике лежат шары: 5 красных, 7 синих и 1 зелёный.

а)

Сколько шаров надо вынуть, чтобы наверняка достать 2 шара одного цвета?

б)

Сколько шаров надо вынуть, чтобы наверняка достать 2 шара разного цвета?

Дополнительные задачи

6.

Сколько раз за сутки минутная стрелка обгоняет часовую?

7.

Таблица 9×9 заполнена ненулевыми цифрами так, что в каждой строке встречаются все цифры от 1 до 9. Таблица симметрична относительно диагонали, соединяющей левый верхний и правый нижний углы таблицы. Докажите, что на этой диагонали есть цифра 7.

8.

В межпланетном шахматном турнире в Нью-Васюках, проводившемся по круговой системе, за победу давали 2 очка, за ничью 1 очко, за поражение — 0 очков. Гроссмейстер Остап Бендер одержал больше всех побед. Мог ли он набрать меньше всех очков?

9.

Будем по очереди закрашивать поля доски 8×8 в красный цвет так, чтобы после закрашивания каждой следующей клетки фигура, состоящая из закрашенных клеток, имела ось симметрии. Покажите, как можно закрасить а) 26, б) 28 клеток, соблюдая это условие.