МАЛЫЙ МЕХМАТ МГУ

Кружок 6 класса

Занятие 16. Последовательности

1.

Найдите сумму:

а)

всех натуральных чисел от 1 до 50;

б)

всех двузначных чисел;

в)

всех четырёхзначных чисел.

Ответ Решение

Ответ. а) 1275; б) 4905; в) 49495500.

Решение.

а) Обозначим искомую сумму S:
S = 1 + 2 + 3 + ... + 50
Теперь запишем ту же сумму в обратном порядке:
S = 50 + 49 + 48 + ... + 1
Напишем эти формулы одну под другой и «сложим в столбик», складывая слагаемые, написанные друг под другом:
S = 1 + 2 + 3 + ... + 50
S = 50 + 49 + 48 + ... + 1
2S = 51 + 51 + 51 + ... + 51
В последней сумме 50 слагаемых (как и в исходной сумме), поэтому 2S = 51·50, откуда S = 51 · 50 : 2 = 1275.

б) Решаем аналогично пункту а:
S = 10 + 11 + 12 + ... + 99
S = 99 + 98 + 97 + ... + 10
2S = 109 + 109 + 109 + ... + 109
В последней сумме 90 слагаемых (именно столько существует двузначных чисел и именно столько слагаемых в исходной сумме), поэтому 2S = 109·90, откуда S = 109 · 90 : 2 = 4905.

в) Решаем аналогично пунктам а и б:
S = 1000 + 1001 + 1002 + ... + 9999
S = 9999 + 9998 + 9997 + ... + 1000
2S = 1099 + 1099 + 1099 + ... + 1099
В последней сумме 9000 слагаемых (именно столько существует четырёхзначных чисел и именно столько слагаемых в исходной сумме), поэтому 2S = 1099·9000, откуда S = 1099 · 9000 : 2 = 49495500.

2.

Делится ли на 2013 сумма 1 + 2 + 3 + ... + 2013?

Ответ Решение

Ответ. Делится.

Решение. Получим более простое выражение для искомой суммы, действуя по аналогии с задачей 1.
S = 1 + 2 + 3 + ... + 2013
S = 2013 + 2012 + 2011 + ... + 1
2S = 2014 + 2014 + 2014 + ... + 2014
В последней сумме 2013 слагаемых (как и в исходной сумме), поэтому 2S = 2014·2013, откуда S = 2014 · 2013 : 2 = 1007 · 2013. Из последнего равенства следует, что сумма S делится на 2013.

3.

Найдите сумму:

а)

всех нечётных чисел от 1 до 100;

б)

всех натуральных чисел от 1 до 150, делящихся на 3;

в)

всех натуральных чисел, не превосходящих 80 и делящихся на 6 с остатком 1.

Ответ Решение

Ответ. а) 2500; б) 3825; в) 560.

Решение.

Будем решать эту задачу по аналогии с задачей 1.

а) Обозначим искомую сумму S:
S = 1 + 3 + 5 + ... + 99
S = 99 + 97 + 95 + ... + 1
2S = 100 + 100 + 100 + ... + 100
В последней сумме 50 слагаемых (как и в исходной сумме: среди 100 чисел от 1 до 100 ровно половина нечётных), поэтому 2S = 100·50, откуда S = 100 · 50 : 2 = 2500.

б) Решаем аналогично пункту а:
S = 3 + 6 + 9 + ... + 150
S = 150 + 147 + 144 + ... + 3
2S = 153 + 153 + 153 + ... + 153
В последней сумме 150 : 3 = 50 слагаемых (как и в исходной сумме: среди 150 чисел от 1 до 150 ровно треть делится на 3), поэтому 2S = 153·50, откуда S = 153 · 50 : 2 = 3825.

в) Решаем аналогично пунктам а и б:
S = 1 + 7 + 13 + ... + 79
S = 79 + 73 + 67 + ... + 1
2S = 80 + 80 + 80 + ... + 80
В последней сумме 14 слагаемых (как и в исходной сумме: неполные частные от деления этих чисел на 6 равны, соответственно, 0, 1, 2, ..., 13), поэтому 2S = 80·14, откуда S = 80 · 14 : 2 = 560.
Обратите внимание: поскольку 1 = 6·0 + 1, число 1 тоже делится на 6 с остатком 1 (и неполным частным 0).

4.

На клетчатой бумаге нарисована фигура (см. рисунок): в верхнем ряду — одна клеточка, во втором сверху — три клеточки, в следующем ряду — 5 клеточек, и так далее. Сколько всего в этой фигуре клеточек, если в ней:

а)

5 рядов;

б)

25 рядов;

в)

2013 рядов?

Ответ Решение

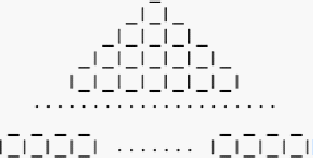
Ответ. а) 5² = 25; б) 25² = 625; в) 2013² = 4052169.

Решение.

Число клеток в k-м ряду фигуры равно k-му нечётному числу. Значит, площадь такой фигуры из n рядов равна сумме первых n нечётных чисел.

а) 1 + 3 + 5 + 7 + 9 = 25.

б) Двадцать пятое нечётное число — это число 49. Аналогично задаче 1 вычислим, что 1 + 3 + 5 + ... + 49 = (1 + 49) · 25 : 2 = 25² = 625.

в) Заметим, что число клеток в такой фигуре всегда равно квадрату числа рядов. Это легче всего заметить геометрически (см. рисунок ниже).

Для этого часть фигуры, закрашенную красным, отрежем и приложим к фигуре с другой стороны (часть, закрашенная зелёным). В результате получится квадрат, число клеток в стороне которого равно количеству рядов в исходной фигуре. Площадь этого квадрата, с одной стороны, равна площади исходной фигуры, а с другой стороны, равна квадрату количества рядов в исходной фигуре. В частности, если фигура состоит из 2013 рядов, то количество клеток в ней равно 2013² = 4052169.

Можно получить тот же результат и иначе. Заметим, что k-е нечётное число равно (2k−1) (проверьте!). Таким образом, если фигура состоит из n рядов, число клеток в ней равно сумме нечётных чисел от 1 до (2n−1). Вычислим эту сумму:
S = 1 + 3 + 5 + ... + (2n−1)
S = (2n−1) + (2n−3) + (2n−5) + ... + 1
2S = 2n + 2n + 2n + ... 2n = 2n·n
S = n·n = n².

final: Последовательность Фибоначчи — такая последовательность натуральных чисел, в которой первые два числа — единицы, а каждое следующее число равно сумме двух предыдущих: 1, 1, 2, 3, 5, 8, 13, 21, 34, ... .

5.

Некто приобрёл пару кроликов и поместил их в загон. Сколько кроликов будет в загоне через год, если считать, что каждый месяц пара дает в качестве приплода новую пару кроликов, которые со второго месяца жизни также начинают приносить приплод?

Ответ Решение

Ответ. 377 пар.

Решение. Каждая пара, родившаяся два месяца назад, в текущем месяце даёт одну новую пару. Каждая пара, родившаяся месяц назад, в текуще месяце приплода не даёт, но у неё есть пара родителей, которые в текущем месяце тоже дадут одну новую пару. Других новых пар кроликов не будет. Поэтому количество новых пар в текущем месяце равно количеству новых пар в прошлом месяце плюс количество новых пар в позапрошлом месяце. Таким образом, числа пар кроликов, родившихся в каждом месяце, образуют последовательность Фибоначчи. Чтобы получить ответ, нужно сложить первые 12 чисел Фибоначчи и ещё добавить к этому одну пару, которую купили вначале. Получим 1 + 1 + 2 + 3 + 5 + 8 + 13 + 21 + 34 + 55 + 89 + 144 + 1 = 377 пар.

6.

а)

Сколько есть способов разрезать полоску 2×3 на доминошки 1×2? Тот же вопрос для полоски:

б)

2×4;

в)

2×5. Полоски нельзя переворачивать.

г)

Даша посчитала число способов разрезания для полоски 2×2013 и вычла из него число способов разрезания для полоски 2×2012. А Таня посчитала число способов разрезания для полоски 2×2011. У кого из них в результате получилось большее число?

Ответ Решение

Ответ. а) 3; б) 5; в) 8; г) у них получились одинаковые числа.

Решение.

а) Очевидно, что полоску 2×1 можно разрезать на доминошки одник способом, а полоску 2×2 — двумя. Далее, если от полоски 2×3 вначале отрезать одну вертикальную доминошку, останется полоска 2×2, которую можно разрезать одним из двух способов (как мы отметили выше). Если же от полоски 2×3 вначале отрезать две горизонтальные доминошки, останется прямоугольник 2×1, который можно разрезать одним способом. Итого полоску 2×3 можно разрезать 2 + 1 = 3 способами.

б) Аналогичным образом поступим с полоской 2×4. Либо мы сначала отрезаем одну вертикальную доминошку, и остаётся прямоугольник 2×3, который можно разрезать пятью способами, либо мы сначала отрезаем две горизонтальные доминошки, и остаётся прямоугольник 2×2, который можно разрезать тремя способами. Итого полоску 2×4 можно разрезать на доминошки 5 + 3 = 8 способами.

в)Рассуждая таким же образом, как в пунктах а и б, посчитаем, что полоску 2×5 можно разрезать 8 + 5 = 13 способами.

Докажем, что (число способов разрезать полоску 2×2013) = (число способов разрезать полоску 2×2012) + (число способов разрезать полоску 2×2011). В самом деле, если сначала отрезать от полоски 2×2013 одну вертикальную доминошку, останется полоска 2×2012, которую ещё надо разрезать; если же сначала отрезать две горизонтальные доминошки, останется разрезать полоску 2×2011. А из этого следует, что Даша и Таня в результате получили одно и то же число.

7.

Может ли сумма первых нескольких подряд идущих натуральных чисел оканчиваться цифрой 7?

Ответ Решение

Ответ. Не может.

Решение.

Вычислим сумму первых n подряд идущих натуральных чисел:
S = 1 + 2 + 3 + ... + n
S = n + (n−1) + (n−2) + ... + 1
2S = (n+1) + (n+1) + (n+1) + ... (n+1) = n·(n+1)
S = n·(n+1) : 2.

Чтобы это число оканчивалось цифрой 7, вдвое большее число n·(n+1) должно оканчиваться цифрой 4 (так как последняя цифра числа 2·7 = 14 равна 4). Последняя цифра произведения двух чисел равна последней цифре произведения их последних цифр (вспомните правило умножения в столбик). Пользуясь этим соображением, составим таблицу:

Последняя цифра числа n	Последняя цифра числа (n+1)	Последняя цифра числа n·(n+1)
0	1	0
1	2	2
2	3	6
3	4	2
4	5	0
5	6	0
6	7	2
7	8	6
8	9	2
9	0	0

В последнем столбце этой таблицы нигде не встречается цифра 4. Значит, число n·(n+1) ни при каких n не может оканчиваться цифрой 4, а число n·(n+1) : 2 ни при каких n не может оканчиваться цифрой 7.

8.

а)

Лёша поднимается по лестнице из 10 ступенек. За один шаг он поднимается вверх либо на одну ступеньку, либо на две ступеньки. Сколькими способами Лёша может подняться по этой лестнице?

б)

При спуске с той же лестницы Лёша перепрыгивает через некоторые ступеньки (может даже через все 10). Сколькими способами он может спуститься по этой лестнице?

Ответ Решение

Ответ. а) 89; б) 2⁹ = 512.

Решение.

а) Обозначим через а_n число способов подняться на лестницу из n ступенек, соблюдая условия задачи. Очевидно, a₁ = 1, a₂ = 2. Пусть Петя запрыгивает на лестницу из n > 2 ступенек. Если первый прыжок был на две ступеньки, то ему осталось запрыгнуть на (n − 2) ступеньки, и число способов закончить подъем равно a_n−2. Если же первый прыжок был на одну ступеньку, то число способов закончить подъем равно a_n−1. Значит, a_n = a_n−1 + a_n−2. Поэтому числа a_n образуют последовательность Фибоначчи: a₃ = 3, a₄ = 5, a₅ = 8, a₆ = 13, a₇ = 21, a₈ = 34, a₉ = 55, a₁₀ = 89.

б) Каждую из 9 ступенек (кроме последней) Петя может либо перепрыгнуть, либо не перепрыгнуть независимо от того, на каких из верхних ступенек он останавливался. Поэтому количество способов спуститься по лестнице равно 2⁹ = 512.