МАЛЫЙ МЕХМАТ МГУ

Кружок 6 класса

Занятие 0. Письменная работа

1.

Делимое вчетверо больше делителя, а делитель вчетверо больше частного. Найдите делимое, делитель и частное.

Ответ Решение

Ответ. 64 : 16 = 4.

Решение.

Первое условие означает, что делимое : делитель = 4. Значит, частное = 4. Тогда делитель = частное · 4 = 16, а делимое = делитель · 4 = 64.

Примечание. Обратите внимание, что решение не зависит от того, о каких числах идёт речь — целых или дробных.

2.

Из Москвы в Новгород послали гонца, и проходит он каждый день 30 вёрст. На другой день следом за ним послали другого гонца, который проходит 35 вёрст в день. Когда второй гонец догонит первого?

Ответ Решение

Ответ. Через 6 дней после того, как второй гонец выйдет из Москвы.

Решение.

К тому моменту, когда второй гонец выходил из Москвы, первый находился от него на расстоянии в 30 вёрст, которое он прошел за предыдущий день. Расстояние между гонцами сокращается со скоростью 35 − 30 = 5 вёрст в день. Значит, второй гонец догонит первого через 30 : 5 = 6 дней после того, как выйдет их Москвы.

Примечание. В условии задачи ничего не говорится о расстоянии между Москвой и Новгородом. Предполагается, что Москва и Новогород достаточно далеко друг от друга, чтобы второй гонец догнал первого ещё в пути, а не в Новгороде. Это вполне согласуется с реальной жизнью. Действительно, от Москвы до Новгорода около 600 км (по прямой; путь по сколько-нибудь приемлемым для пешехода дорогам еще длиннее). За шесть дней пути второй гонец пройдет 35·6 = 210 вёрст. Одна верста соответствует 1066,8 м. Так что к моменту встречи гонцы пройдут чуть больше трети пути от Москвы до Новгорода.

3.

Кузнечик умеет прыгать вдоль заданной прямой на 6 см и на 8 см (в любую сторону). Сможет ли он за несколько прыжков попасть в точку, расстояние от которой до исходной равно:

а)

4 см;

б)

7 см?

Ответ Решение

Ответ. а) Сможет; б) не сможет.

Решение.

а) Для этого кузнечику нужно два раза прыгнуть на 6 см в одну сторону и один раз — на 8 см в другую.

б) Так как 6 и 8 — чётные числа, кузнечик после любого прыжка будет находиться на расстоянии в чётное число сантиметров от исходной точки. А 7 — число нечётное.

4.

На острове живут два племени — рыцари и лжецы (первые всегда говорят правду, вторые — всегда лгут). Путешественник нанял туземца-островитянина в проводники. По дороге они встретили ещё одного островитянина. Путешественник попросил своего проводника узнать, к какому племени принадлежит этот человек. Проводник вернулся и сообщил, что тот назвался рыцарем. Из какого племени мог быть проводник?

Ответ Решение

Ответ. Проводник был рыцарем.

Решение.

Рассмотрим четыре возможных случая.

1. Пусть и встречный, и проводник — рыцари. Тогда встречный назовётся рыцарем, а проводник дословно передаст это путешественнику. Эта ситуация удовлетворяет условию задачи.

2. Пусть встречный — лжец, а проводник — рыцарь. Тогда встречный назовётся рыцарем, а проводник дословно передаст это путешественнику. Эта ситуация также удовлетворяет условию задачи.

3. Пусть встречный — рыцарь, а проводник — лжец. Тогда встречный назовётся рыцарем, а проводник скажет путешественнику, что тот назвался лжецом. Эта ситуация не удовлетворяет условию задачи.

4. Пусть и встречный, и проводник — лжецы. Тогда встречный назовётся рыцарем, а проводник скажет путешественнику, что тот назвался лжецом. Эта ситуация также не удовлетворяет условию задачи.

Таким образом, проводник мог быть только рыцарем. Из какого племени был встречный, определить невозможно.

5.

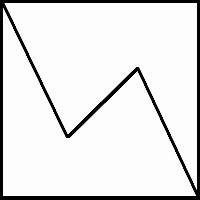
Разрежьте какой-нибудь квадрат на два одинаковых пятиугольника.

Ответ

Ответ. На рисунке ниже приведено одно из возможных решений.

6.

Автомобиль Opel Corsa выпускается с двумя различными типами кузова, тремя различными коробками передач и четырьмя различными двигателями. Сколько всего выпускается модификаций автомобиля Opel Corsa, если любой тип кузова сочетается с любым двигателем и любой коробкой передач?

Ответ Решение

Ответ. 24.

Решение. Есть два способа выбрать тип кузова. При каждом способе выбора кузова есть по три способа выбрать коробку передач. При каждом способе выбрать кузов и коробку передач есть по 4 способа выбрать двигатель. Модификация — это тип кузова, коробки передач и двигателя. Поэтому всего существует 2·3·4 = 24 модификации автомобиля Opel Corsa.

7.

Можно ли клетчатую доску 100×100 разрезать на трёхклеточные уголки? Ответ подробно объясните.

Ответ Решение

Ответ. Нельзя.

Решение. Доска 100×100 состоит из 100·100 = 10000 клеток. Если бы её можно было разрезать на трёхклеточные уголки, то 10000 делилось бы на 3 нацело (и частное было бы равно числу уголков). А поскольку 10000 на 3 нацело не делится, эту доску разрезать на трёхклеточные уголки нельзя.

8.

В парке 10 беседок, и от каждой из них идут тропинки к трём другим беседкам. Сколько всего тропинок соединяет беседки друг с другом? Укажите все возможные варианты.

Ответ Решение

Ответ. 15.

Решение. Будем заходить в каждую беседку и считать тропинки, отходящие от неё. Обойдя все беседки, мы насчитаем 10·3 = 30 тропинок. Но при этом каждую тропинку мы посчитали два раза, ведь она соединяет две беседки. Поэтому для получения правильного ответа нужно это число поделить пополам. 30 : 2 = 15.

9.

а)

Сколько существует натуральных чисел, не превосходящих 1000, которые делятся на 3? На 5? На 15?

б)

Не делятся ни на 3, ни на 5?

Ответ Решение

Ответ. а) 333; 200; 66. б) 533.

Решение.

а) На 3 делится каждое третье натуральное число. Чтобы найти количество таких чисел от 1 до 1000, надо 1000 поделить с остатком на 3 и взять неполное частное. 1000 = 3·333 + 1. Аналогично находим количество натуральных чисел от 1 до 1000, делящихся на 5 (соотвественно, на 15). 1000 = 5·200 = 66·15 + 10.

б) Сначала выясним, сколько натуральных чисел от 1 до 1000 делятся хотя бы на одно из чисел 3 и 5. Из интересующих нас натуральных чисел 333 делятся на 3 и 200 делятся на 5. Если просто сложить 333 + 200 = 533, мы дважды посчитаем числа, которые делятся одновременно на 3 и на 5 (другими словами, которые делятся на 15). Поэтому среди натуральных чисел только 333 + 200 − 66 = 467 делятся хотя бы на одно из чисел 3 и 5. Остальные 1000 − 467 = 533 числа не делятся ни на 3, ни на 5.

10.

Ваня задумал натуральное число, умножил его на 13, зачеркнул последнюю цифру результата, полученное число умножил на 7, зачеркнул последнюю цифру результата и получил 21. Какое число задумал Ваня? Укажите все возможные варианты.

Ответ Решение

Ответ. 24.

Решение. Начнём рассуждать с конца. Число, которое получилось у Вани перед последним зачёркиванием цифры, должно было делиться на 7 (так как было получено из какого-то другого числа умножением на 7). Это могло быть или число 210, или число 217 (другие натуральные числа от 210 до 219 на 7 не делятся). Рассмотрим оба этих случая. Имеем 210 : 7 = 30 и 217 : 7 = 31. Эти числа могли быть получены зачёркиванием последней цифры из какого-то числа, которое делилось на 13. Число 31 могло быть получено таким способом только из числа 312 (другие натуральные числа от 310 до 319 на 13 не делятся). А вот число 30 не могло быть получено таким способом из числа, делящегося на 13: среди натуральных чисел от 300 до 309 нет ни одного, которое делилось бы на 13. Поэтому перед первым зачёркиванием у Вани получилось число 312, которое в 13 раз больше задуманного. Поэтому задуманное число равно 312 : 13 = 24.

11.

Несколько ребят сидели и пили чай с 36 конфетами. Дима сказал: «Я сумею так разделить конфеты, что у каждого из нас будет не больше пяти конфет». Вова ответил ему: «А я могу так разделить конфеты, что каждому хоть что-то достанется и при этом число конфет у всех будет разным!». Сколько ребят пили чай?

Ответ Решение

Ответ. 8.

Решение.

Сначала убедимся, что за столом могло быть 8 человек. Во-первых, можно дать семерым из них по 5 конфет, а восьмому — одну. Тогда все 7·5+1 = 36 конфет будут розданы, и у каждого будет не больше пяти конфет, что и обещал сделать Дима. Во-вторых, можно дать первому человеку одну конфету, второму — две, третьему — три и так далее до восьмого. Всего мы раздадим 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 = 36 конфет. При этом каждому хоть что-то достанется и число конфет у всех будет разным, что и обещал Вова.

Если бы за столом было меньше восьми человек, то Диме не удалось бы выполнить обещанное. В самом деле, если каждому из не более чем семи человек дать не более пяти конфет, то всего будет роздано не более 7·5 = 35 конфет.

Если бы за столом было больше восьми человек, то обещанное не удалось бы выполнить уже Вове. Сначала будем стараться выполнить обещание Вовы, давая каждому как можно меньше конфет. Первому человеку дадим одну конфету (меньше ему дать нельзя, ведь каждому должно что-то достаться). Тогда второму человеку нужно дать больше одной конфеты, ведь у всех должно быть разное число конфет. Поэтому дадим второму человеку две конфеты. Рассуждая аналогично, дадим третьему три конфеты, четвёртому — четыре и так далее. Восьмому человеку достанется 8 конфет; теперь все 36 конфет розданы, и остальным ничего не достанется. Если же раздавать конфеты более щедро, то больше чем на 8 человек их тем более не хватит (если стараться выполнить обещание Вовы).

12.

В детском саду в группе из 50 детей некоторые знают все буквы, кроме «р», которую просто пропускают при письме, а остальные знают все буквы, кроме «к», которую тоже пропускают. Однажды воспитатель попросил 10 детей написать слово «кот», 18 других детей — слово «рот», а остальных — слово «крот». При этом слова «кот» и «рот» оказались написаны по 15 раз. Сколько ребят написали своё слово верно?

Ответ Решение

Ответ. 8.

Решение.

Никто из тех, кто должен был написать слово «крот», не мог этого сделать верно: никто из детей в группе не умеет одновременно писать и букву «р», и букву «к». Поэтому эти дети вместо слова «крот» в общей сложности написали 50 − 10 − 18 = 22 неверных слова «кот» и «рот».

Те, кто написал не «кот» и не «рот», могли написать только слово «от», которое явно неправильное. Таких было 50 − 15 − 15 = 20 человек.

Наконец, осталось 50 − 22 − 20 = 8 человек, которые написали слово «кот» или слово «рот» правильно.