
|
Занятие 3. ГНОМИКИ И КОМБИНАТОРИКА
|
0. | a) В магазине
"Гномик-мода" новая коллекция
осенней одежды. Продаются 123 различных плащa
и 321 колпак. Гномик Веня пришел в магазин
и растерялся: сколько же способов подобрать
себе наряд! А действительно, сколько?
b) В отделе женской одежды неразбериха еще
больше: 1234 модели плаща, 4321 модель колпаков
567 моделей левого ботинка и 765 - правого.
Сколькими способами может одеться гномик Маня?
|
Ответ
Решение
|
|
Ответ.
a) 123×321 способ,
b) 1234×4321×567×765.
|
|
|
|
|
Решение.
a) Плащ гномик может выбрать 123 способом.
После того как он выбрал плащ, колпак он может выбрать
321 способом. То есть для каждого выбранного плаща
у нас есть 321 способ выбрать колпак. Поэтому, всего
321 + 321 + ... + 321 = 123×321 способа.
b) Решается точно-также. Плащ и колпак можно выбрать
1234×4321 способами. На каждый выбор плаща и
колпака можно выбрать 567 моделей левого ботинка.
Всего таких наборов 1234×4321×567.
Добавив еще выбор правого ботинка, получаем еще один
множитель: 1234×4321×567×765.
|
|
|
|
| |
1. | Гномик Веня готовит
пиццу. У него есть такие начинки:
перец, лук, ветчина, грибы, огурцы и помидоры.
Каждую он может использовать или нет. Кроме того, он
может приготовить пиццу вообще без начинок. Сколько
рецептов пиццы знает Веня?
|
Ответ
Указание
|
|
|
|
Указание.
Эта задача имеет много общего с
задачей 0.b. Надо совершить выбор столько раз,
сколько у нас начинок. Каждую либо берём, либо
нет. Можно сказать так: есть две модели первой
начинки - есть перец, нет перца, две модели второй
начинки - есть лук, нет лука и так далее...
|
|
|
|
| |
2. | Приготовив пиццу,
Веня решил разделить ее между
гномиками. На какое максимальное число частей он
может разделить ее четырьмя прямыми разрезами, если
a) после разрезания куски нельзя перекладывать
b) перекладывать куски можно?
| |
3. | В Волшебном
лесу живут 2003 гномика. Никакие три
домика гномиков не разположены на одной прямой. Каждая
пара домиков гномиков соединена дорогой. Сколько
дорог в лесу?
|
Ответ
Указание
|
|
Ответ.
(2003×2002)/2 дороги
|
|
|
|
|
Указание.
У каждой дороги есть 2 конца, каждый у
какого-нибудь домика. Если мы посчитаем, сколько
концов у всех дорог и разделим это число попалам,
то мы как раз и получим число дорог.
Посчитаем теперь сколько у нас концов дорог.
В каждый домик ведут дороги из всех других домиков,
то есть 2002 дороги, значит около каждого доми 2002
конуа дорог. Всего домиков 2003, значит,
всего концов 2003×2002.
А дорог всего (2003×2002)/2.
|
|
|
|
| |
4. | Глядя
на карту Волшебного леса, Маня воскликнула:
"Ой, как много дорог! Интересно, а сколько
треугольников с вершинами-домиками нарисовано на карте?"
Помогите Мане подсчитать их.
|
Ioaao
Oeacaiea
|
|
Ioaao.
(2003×2002×2001)/(3×2×1)
|
|
|
|
|
Oeacaiea.
Нужно посчитать, сколькими способами мы можем
выбрать три домика (вершины треугольника) из 2003.
Первый домик мы можем выбрать 2003 способами.
После того, как мы выбрали первый домик, у нас есть 2002
кандидата на выбор второго домика (один домик мы уже не модем выбрать,
так как он выбран первым.) После того, как выбрали второй
домик, у нас есть 2001 способ выбрать третий.
И так, у нас есть 2003×2002×2001
способов выбрать первую, вторую и третью вершины.
Но тут мы учитывали, в каком порядке мы выбирали домики-вершины.
Но, на самом деле, нам это не важно. И если мы будем
выбирать домики-вершины в другом порядке, то полученный треугольник
не изменится. Значит, всего способов выбрать треугольник меньше.
Давайте посчитаем, сколько способов выбрать первую, вторую и третью
вершины преведут к одному треугольнику.
Сколько у нас есть способов три домика расставить по порядку?
На первом месте может стоять один из трёх домиков,
на втором --- один из оставшихся 2, на третьем --- оставшийся 1 домик.
Значит, всего 3×2×1 способ расставить три домика по
порядку. И так у нас 3×2×1 способов выбора
домиков-вершин приводит к одному и тому-же треугольнику.
Следовательно, всего (2003×2002×2001)/(3×2×1)
способов выбрать вершины треугольника.
|
|
|
|
| |
5. | 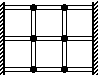 Посередине
Волшебной речки расположены шесть
островов так как показано на рисунке. Также
нaрисована система
мостов между ними. Подсчитайте, сколько существует
способов перейти реку, не возвращаясь на тот берег,
с которого начали и не проходя через
один остров более одного раза. Посередине
Волшебной речки расположены шесть
островов так как показано на рисунке. Также
нaрисована система
мостов между ними. Подсчитайте, сколько существует
способов перейти реку, не возвращаясь на тот берег,
с которого начали и не проходя через
один остров более одного раза.
| |
6. | Перед
домиком гномика Сени крыльцо с 23 ступеньками.
Когда гномик поднимается по лестнице, он либо наступает
на каждую ступеньку, либо перепрыгивает через одну.
Сколько гномиков могут прийти к Сене в гости, если они
все будут подниматься разными способами?
| |
7. | У модницы
Мани 3 ягоды брусники и 7 ягод клюквы.
Каждый день она делает себе из них ожерелье, используя
все 10 ягод как бусинки, и идет
на дискотеку гномиков. Сколько дней подряд Маня
может делать себе разные ожерелья? (Если ожерелье
повернуть, то это будет то же самое ожерелье, а если
перевернуть, то другое)
| |
8. | Гномик-шахтер
Веня нашел 14 изумрудов и 7 алмазов.
У него есть 19 братьев и 2 сестры: Маня и Таня.
Он хочет подарить всем по камешку, но так, чтобы
хотя бы один алмаз достался девочке. Сколько
существует способов разделить драгоценности?
|
|


 Посередине
Волшебной речки расположены шесть
островов так как показано на рисунке. Также
нaрисована система
мостов между ними. Подсчитайте, сколько существует
способов перейти реку, не возвращаясь на тот берег,
с которого начали и не проходя через
один остров более одного раза.
Посередине
Волшебной речки расположены шесть
островов так как показано на рисунке. Также
нaрисована система
мостов между ними. Подсчитайте, сколько существует
способов перейти реку, не возвращаясь на тот берег,
с которого начали и не проходя через
один остров более одного раза.