МАЛЫЙ МЕХМАТ МГУ

Кружок 7 класса

Занятие 8 (15 ноября 2014 года). Эйлеровы графы.

1.

Нарисуйте фигуры, изображенные на рисунке, не отрывая карандаша от бумаги и не проводя никакую линию дважды.

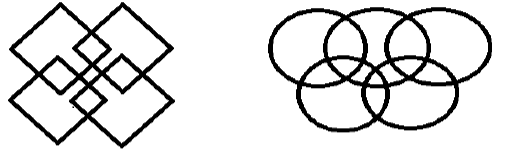
2.

В стране имеется несколько городов, некоторые из которых соединены дорогами, причем из города Шарамбарам выходит ровно n дорог. Известный путешественник выехал из одного из городов и объехал всю страну, проехав по каждой дороге ровно один раз. Закончился ли его путь в Шарамбараме, если

1. он начал путь в городе Шарамбарам и n чётно;
2. он начал путь в городе Шарамбарам и n нечётно;
3. он начал путь в другом городе и n чётно;
4. он начал путь в другом городе и n нечётно?

3.

Задача Эйлера о Кенигсбергских мостах. Через город Кенигсберг протекает река, в русле которой расположены два острова. С большего острова ведет по два моста на каждый из берегов и один мост на меньший остров. Кроме этого моста с меньшего острова ведет по одному мосту на каждый из берегов. Некто хочет совершить прогулку по городу, пройдя по каждому мосту ровно один раз. Удастся ли ему это?

Определение. Путь, содержащий все ребра графа, называется эйлеровым путем.

4.

Докажите, что если в графе более двух вершин с нечетными степенями, то в этом графе нет эйлерова пути.

5.

Докажите, что если в графе степени всех вершин чётны, то в этом графе есть цикл.

6.

Докажите, что если в графе степени всех вершин чётны, то рёбра этого графа можно разбить на несколько циклов.

7.

Докажите, что если два цикла имеют общую вершину, то их можно объединить в один самопересекающийся цикл.

8.

Докажите, что если в связном графе степени всех вершин чётны, то в этом графе есть эйлеров цикл.

9.

Докажите, что если в связном графе ровно две вершины с нечетными степенями, то в этом графе есть эйлеров путь.

10.

При каких n правильный n-угольник со всеми его диагоналями можно нарисовать не отрывая карандаша?

11.

Город представляет из себя квадрат 3 на 3, в котором каждая сторона квартала-квадратика — участок улицы длиной 300 метров. Какой наименьший путь придётся проделать катку, чтобы заасфальтировать улицы?