МАЛЫЙ МЕХМАТ МГУ

Кружок 7 класса

Занятие 14 (21 февраля 2015 года). Всякая всячина.

1.

Расставьте числа в клетках изображенной на рисунке фигуры так, чтобы в любом прямоугольнике из трех клеток сумма чисел была равна 1, и сумма всех чисел была равна 1. (Достаточно привести один пример.)

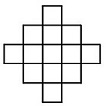
2.

Каждый из семи фальшивомонетчиков изготовил по 31 монете: 20 монет по 6 рублей, 10 — по 1 рублю и 1 монету в 5 рублей. Любые двое могут меняться монетами так, чтобы у каждого оставалась такая же сумма денег. Могут ли в результате таких обменов все монеты по 1 рублю оказаться у одного фальшивомонетчика?
Не забудьте обосновать свой ответ.

3.

На доске было написано число 141. Каждую минуту у написанного на доске числа перемножают все цифры и полученное произведение либо прибавляют к числу, либо вычитают из него (а результат записывают на доску вместо исходного числа). Докажите, что число 141 больше никогда не появится на доске.

4.

У каждого марсианина три руки и несколько антенн. Каждый марсианин взял за руки трех других (так что все руки оказались заняты). Оказалось, что у любых двух из марсиан, взявшихся за руки, количество антенн отличается ровно в 6 раз. Может ли суммарное количество антенн у марсиан быть ровно 2006?

5.

Саша и Федя написали на 1000 карточках числа от 0 до 999, после чего разделили карточки между собой. Каждый из них выложил свои карточки в ряд и получил длинное число. Могут ли длинные числа у Саши и Феди совпасть?

6.

У 10 девочек было по 10 конфет. Каждая девочка подарила несколько конфет другим (конфеты, полученные в подарок, девочки оставляют себе). В результате у всех девочек оказалось разное число конфет. Докажите, что какая-то из девочек подарила конфет не меньше, чем у нее их оказалось в конце.

7.

Костя написал два числа, не содержащих в записи нулей, и заменил цифры буквами (разные цифры — разными буквами). Оказалось, что число КРОКОДИЛЛЛ делится на 312. Докажите, что число ГОРИЛЛА не делится на 392.

8.

Дед Мороз подарил каждому из 102 детей по 100 конфет. Конфеты бывают трех видов: красные, синие и зеленые. Докажите, что найдутся двое, чьи наборы конфет либо полностью одинаковы, либо полностью различны. (Два набора конфет считаются полностью одинаковыми, если в них поровну конфет каждого вида, и полностью различными, если никакого вида конфет в них не поровну.)