МАЛЫЙ МЕХМАТ МГУ

Кружок 7 класса
Руководители Екатерина и Евгений Адищевы
2005/2006 учебный год
2005/2006 учебный год
Листок 2. Режем — пилим и кое-что о земельном праве
- 1.
-
- a)
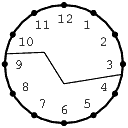
- Однажды волшебный заяц уронил свои часы. Циферблат зазвенел и раскололся на две части. Посмотрев на части, заяц заметил, что суммы чисел, оставшихся в каждой из них, совпадают. Нарисуйте, на какие части мог расколоться циферблат.
Общее указание. Сначала вычислите сумму, которую надо получить на каждом обломке.- b)
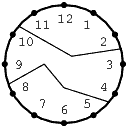
- А мог бы циферблат расколоться на три части, так чтобы сумма чисел в каждой части была одинаковой? А расколоться c) на две, d) на три части так, чтобы сумма цифр в каждой части была одинаковой?
Ответ c. Не могРешение c.Поскольку сумма цифр в каждой части одинакова, то сумма всех цифр циферблата должна делиться на 2. Считаем:
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + (1 + 0) + (1 + 1) + (1 + 2) =
= 45 + 1 + 2 + 3 = 51.Получили нечётное число. Разделить его на две одинаковых части не получится.
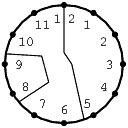
Ответ: не мог.Подсказка1 d. Решение существует, но хитрое.Подсказка2 d. Если разлом пройдёт между единицей и двойкой в числе 12, то они окажутся в разных частях. - 2.
-
Шахматист Волк очень любит играть в шахматы, но ещё больше он любит играть с шахматной доской.
Одна из его любимых игр это распиливание шахматной доски 8×8 на одинаковые части.
Сможет ли он разрезать доску
- a)
- на доминошки размером 1×2
Ответ. Сможет.- b)
- на трёхклеточные уголки (
 )?
)?
Указание. Посчитайте количество уголков, на которые будет разрезана доска.Ответ. Не сможет. - 3.
-
У совы есть ковёр 4×4 метра. Моль проела в нём
15 дырок (каждая дыра — точкa). Может ли сова
вырезать из ковра маленький целый коврик размером 1×1 метр?
Ответ. Может при любом расположении дырок.
- 4.
-
Король Прямоугольного государства (оно находится совсем недалеко
от волшебного леса) провёл на карте своей страны
несколько прямых по линейке от края до края. Государство
оказалось разделено на области. Сможет ли он так раздать
области своим князьям и графам, чтобы соседями князей были
только графы, а соседями графов — князья? (Если границы двух областей
имеют только одну общую точку, то такие области не считаем соседними.)
Ответ. Сможет.
- 5.
-
Может ли король из предыдущей задачи оставить одну область себе,
чтобы среди его соседей были и князья, и графы?
Ответ. Зависит от деления. Нарисуйте деление, при котором такая раздача земли возможна, и деление, при котором она невожможна.
- 6.
-
У князя Квадратной земли есть два сына, которые мечтают стать князьями a) Пятиугольных
b) Шестиугольных c) Семиугольных земель. Сможет ли князь разделить свои владения между ними поровну
(земли должны не только иметь одинаковую площадь, но и совпадать по форме) и исполнить их желания?
Ответ. Сможет во всех трёх случаях.Решение.
a) b) c) 


- 7.
-
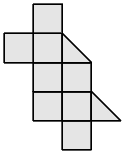
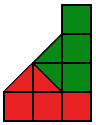
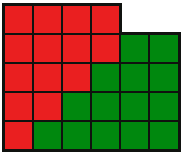
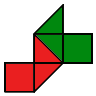
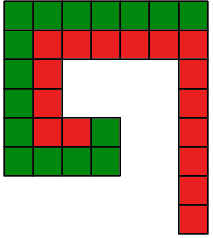
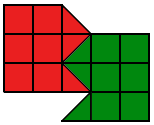
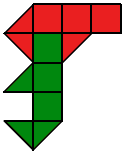
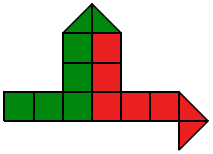
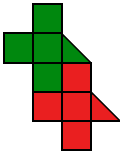
Разрежьте каждую из фигур на две части, одинаковые по форме и размеру.
- a)
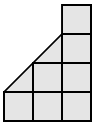
- b)
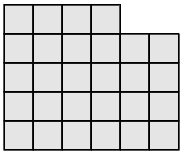
- c)
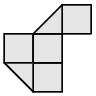
- d)
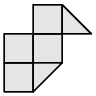
- e)
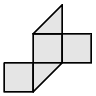
- f)
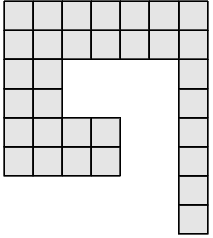
- g)
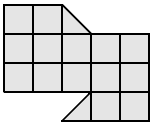
- h)

- i)
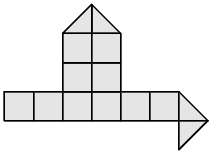
- j)