МАЛЫЙ МЕХМАТ МГУ

Кружок 8 класса

Занятие 20 (5 апреля 2014 года). Вписанные углы

Упражнения:

1.

Докажите, что вписанный угол равен половине меры градусной дуги, на которую он опирается:

а)

одна из сторон угла проходит через центр окружности;

б)

произвольный вписанный угол.

2.

Докажите, что вписанный угол между касательной и хордой, проходящими через одну точку окружности, равен половине дуги, стягиваемой хордой.

Задачи:

Определение. Вневписанный угол λ — угол, образованный двумя прямыми (AB и CD), пересекающими окружность (рис. 1, 2).

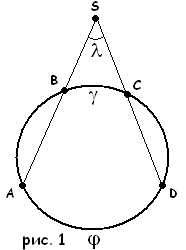
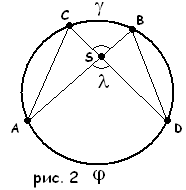
1.

Выразите вневписанный угол λ через углы γ и ϕ

а)

в случае рис. 1;

б)

в случае рис. 2.

2.

(Критерий вписанности четырёхугольника) Четырёхугольник вписан в окружность тогда и только тогда, когда сумма противоположных углов равна 180°.

3.

Шестиугольник ABCDEF — вписанный (все его вершины лежат на одной окружности), причём AB ∥ DE и BC ∥ EF. Докажите, что CD ∥ AF.

Определение. Вписанная N-конечная k-звезда — звезда, построенная следующим образом: на окружности берётся N пронумерованных по часовой стрелке точек, первую вершину соединяем с (k+1)-й, (k+1)-ю — c (2k+1)-й и т. д.

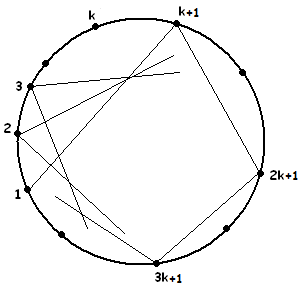
4.

Нарисуйте вписанную 7-конечную 2-звезду и найдите сумму её углов.

5.

Найдите сумму углов вписанной N-конечной k-звезды.

6.

Найдите сумму углов 2014-конечной 3-звезды и 100500-конечной 7-звезды.

7.

(Прямая Симсона) Докажите, что основания перпендикуляров, опущенных из произвольной точки описанной окружности на стороны треугольника (или их продолжения), лежат на одной прямой.

8.

(Задача Архимеда) В дугу AB окружности вписана ломаная AMB из двух отрезков (AM > MB). Докажите, что основание перпендикуляра KH, опущенного из середины K дуги AB на отрезок AM, делит ломаную пополам, т.е. AH = HM + MB.