МАЛЫЙ МЕХМАТ МГУ

Кружок 6 класса

Занятие 20 (1 апреля 2017 года). Первое апреля

В этом листочке все задачи уже решены! Вот только некоторые решения содержат ошибки. Ваша задача — найти эти ошибки (и исправить, если это возможно). Будьте внимательны: в листочке есть и верные решения!

1.

Докажите, что: а) 2 + 2 = 5; б) 2 · 2 = 5.

Решение. а) Очевидно, что 0 = 0. Также очевидно, что 2 · (5 + 5) – 2 · (5 + 5) = 0 и 5 · 5 – 5 · 5 = 0. Отсюда получаем, что 2 · (5 + 5) – 2 · (5 + 5) = 5 · 5 – 5 · 5. Раскрыв скобки и произведя группировку некоторых слагаемых, получим 2 · (5 – 5) + 2 · (5 – 5) = 5 · (5 – 5), или (2 + 2) · (5 – 5) = 5 · (5 – 5) Сократим общий множитель и получим, что 2 + 2 = 5, что и требовалось доказать. б) Из пункта а) следует, что 2 + 2 = 5, но 2 + 2 = 2 · 2. Поэтому 2 · 2 = 5.

2.

Мальвина сказала Буратино умножить число на 9 и к результату прибавить 15, а Буратино умножил число на 15, а потом прибавил 9, но ответ получил верный. Какое это было число?

Решение. Обозначим искомое число через x и составим уравнение: 9x + 15 = 15x + 9. Перенесём x вправо, а числа влево. Получим 24 = 6x. Отсюда x = 4.

3.

Если Аня идёт в школу пешком, а обратно едет на автобусе, то всего на дорогу она тратит 1,5 часа. Если же она едет на автобусе в оба конца, то весь путь у неё занимает 30 минут. Сколько времени потратит Аня на дорогу, если и в школу, и из школы она будет идти пешком?

Решение. На путь пешком в оба конца плюс путь на автобусе в оба конца уйдёт столько же времени, сколько на два пути пешком и на автобусе. Поэтому на дорогу туда-обратно пешком Аня потратит 2 · 1,5 − 0,5 = 2,5 часа.

4.

Петя с другом пошли в тир. Уговор был такой: Пете даются 10 патронов, и за каждое попадание в цель он получает ещё три патрона. Петя стрелял, пока патроны не кончились, и сделал всего 34 выстрела. Сколько раз он попал в цель?

Решение. У Пети было патронов на 10 выстрелов, а выстрелил он 34 раза, значит, 24 патрона он получил дополнительно. Заметим, что при каждом попадании общее количество патронов у Пети увеличивается на 2: один патрон он тратит на выстрел, но получает три патрона взамен. Значит, Петя попал в цель 24 : 2 = 12 раз.

5.

Можно ли на доске 10×10 расставить 13 кораблей 1×4 для игры в «морской бой»? Корабли не должны соприкасаться друг с другом ни сторонами, ни углами.

Решение. Посмотрим, сколько клеточек занимает каждый корабль. Так как он не должен соприкасаться с другими кораблями ни сторонами, ни углами, очертим вокруг него границу шириной в половину клеточки. Таким образом, каждый корабль занимает 4 + 4 + 1 = 9 клеточек. С другой стороны, доска 10×10 даёт нам 100 + 10 + 10 = 120 клеточек (с учётом тех самых «границ»). 13 · 9 = 117 < 120. Значит, 13 кораблей расставить можно.

6.

В универмаге нарядили несколько новогодних ёлок. На 12 из них есть красные шары, на 11 — жёлтые, на 19 — синие, на 6 — красные и жёлтые, на 8 — красные и синие, на 7 — жёлтые и синие, а на одной — шары всех трёх цветов. Сколько ёлок нарядили в универмаге?

Решение. Сложим 12 + 11 + 19 = 42. При этом мы посчитали ёлки, на которых висят шары двух цветов, по два раза. Вычтем их количества из полученной суммы по одному разу: 42 − 6 − 8 − 7 = 21. Теперь никакие ёлки не посчитаны дважды. Однако теперь получается, что ёлку с шарами трёх цветов мы сначала три раза посчитали, а потом три раза вычли, то есть она у нас сейчас не учтена вовсе. Добавив её, получим 21 + 1 = 22 ёлки.

7.

Докажите, что 64 = 65.

Решение. Разрежем треугольник с дыркой площади 64 на части и сложим треугольник без дырки, площади 64. (Площадь прямоугольного треугольника равна половине произведения длин катетов, то есть сторон, прилежащих к прямому углу. Это следует из того, что такой треугольник составляет половину прямоугольника, стороны которого равны катетам треугольника.)

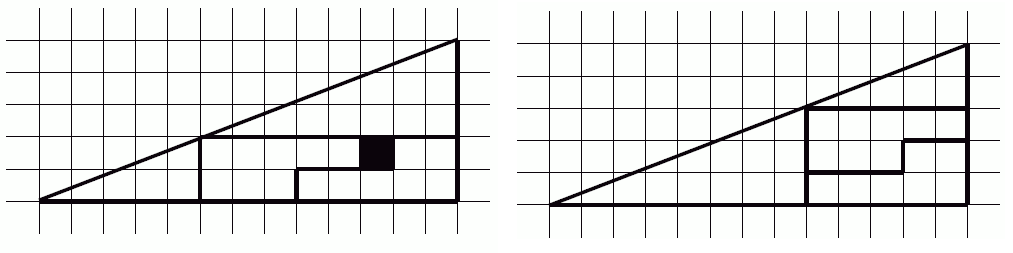
8.

В воскресенье вечером одноклассники звонили друг другу, чтобы узнать домашнее задание. Известно, что каждый ответил по крайней мере на 10 звонков. Также известно, что никакие два одноклассника не разговаривали друг с другом за вечер больше одного раза. Какое наименьшее количество учеников может быть в классе?

Решение. Возьмём одного человека. Ему позвонили ещё минимум 10 разных людей (пусть это будут 2-й, 3-й, 4-й, …, 11-й); итого уже 11 человек. Возьмём второго. Первый ему звонить уже не может — они уже поговорили. Пусть ему позвонят все с 3-го по 11-го — это 9 человек; тогда нужен ещё 12-й, чтобы второму позвонили 10. (Если второму позвонят не все с 3-го по 11-го, то придётся добавить больше новых людей, тогда и общее количество не будет минимальным.) Продолжая эти рассуждения дальше, получим, что требуется минимум 21 человек.