МАЛЫЙ МЕХМАТ МГУ

Кружок 4 класса

Руководитель Александра Ефремовна Подгайц
2014/2015 учебный год

Занятие 19 (28 марта 2015 года). Игра "Обмен"

Правила игры. Каждый игрок получает по одной задаче и бланк для ответов. После того, как задача решена и ответ вписан в бланк, нужно поменяться условием задачи с другим игроком (меняться можно только листочками с условием, ответами и решениями обмениваться нельзя!). Нужно постараться собрать и решить все задачи. Выигрывает тот, у кого в конце игры решено больше всех задач (то есть получен правильныый ответ).

1.: В классе 20 пловцов, 14 борцов и 10 футболистов. Каждый спортсмен занимается ровно двумя из этих видов спорта. Сколько всего в классе спортсменов?
Ответ

Ответ. 22
2.: Лёша хочет вычеркнуть из числа 1329870 три цифры так, чтобы получилось наименьшее число. Покажите, как ему это сделать.
Ответ

Ответ. 1270
3.: Вот несколько числительных, записанных по-венгерски: 43 - negyven három, 58 - ötven nyolc, 375 - háromszáz hetven öt, 197 - száz kilencven hét, 246 - kétszáz negyven hat, 284 - kétszáz nyolcven négy Запишите цифрами: háromszáz negyven nyolc.
Ответ

Ответ. 348
4.: Пятачок, Иа-Иа и Винни-Пух считали морковки на двух грядках Кролика: Пятачок: «На первой грядке морковок больше 18. На второй — не больше 14». Иа-Иа: «На первой меньше 20. На второй ровно 14». Винни-Пух: «На первой ровно 17. На второй больше 14». Известно, что один из них оба раза ошибся, а два других оба раза были правы. Сколько морковок на грядках (обеих в сумме)?
Ответ

Ответ. 33
5.: Несколько гномов, навьючив свою поклажу на пони, отправились в дальний путь. Их заметили тролли, которые насчитали в караване 36 ног и 15 голов. Сколько было гномов, и сколько пони?
Ответ

Ответ. 3 пони, 12 гномов
6.: На чертеже изображён маршрут лыжной прогулки и некоторые расстояния (в км) между поворотами. Найдите полную длину дистанции лыжников.

Ответ

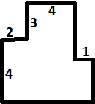Ответ. 28
7.: После того, как туристы прошли 1 км, а затем половину оставшегося пути, им осталось пройти треть всего пути и 1 км. Чему равен весь путь?
Ответ

Ответ. 9 км
8.: Сколько раз за сутки минутная стрелка обгоняет часовую?
Ответ

Ответ. 22
9.: Какой цифрой заканчивается разность 1·2·3·4·….·2012·2013·2014 – 1·3·5·….·2011·2013 ?
Ответ

Ответ. 5
10.: На доске нарисованы два круга, внутри которых отмечено несколько точек. Внутри первго из них всего 190 отмеченных точек. Внутри второго — всего 230 отмеченные точки. Внутри обоих кругов одновременно находится ровно 70 точек. А сколько отмеченных точек всего?
Ответ

Ответ. 350
11.: Александра Ефремовна загадала число от 7 до 70. Ей можно задавать вопросы, на которые можно ответить «да» или «нет». Сколько вопросов понадобится, чтобы гарантированно отгадать число?
Ответ

Ответ. 6
12.: Под крышкой каждой бутылки мехмат-колы нарисована одна из трех картинок: звездочка, карандаш или рожица. Если собрать две крышки с одинаковыми картинками, то их можно обменять в буфете на шоколадку. Сколько бутылок надо купить, чтобы точно получить две шоколадки?
Ответ

Ответ. 6
13.: Каникулы начались 2 июля, а закончились 29 августа. Сколько дней длились каникулы?
Ответ

Ответ. 59
14.: У Насти и Ани денег поровну. Сколько денег должна дать одна из них другой, чтобы у Насти стало на 10 рублей больше, чем у Ани?
Ответ

Ответ. 5
15.: Три землекопа за 2 часа вырыли 3 ямы. Сколько ям выроют 6 землекопов за 5 часов?
Ответ

Ответ. 15

Вы видите ошибку? Выделите её и нажмите Ctrl+Enter!