
МАЛЫЙ МЕХМАТ МГУ

Кружок 8 класса
2010/2011 учебный год
Занятие 6. Неравенства в треугольнике
На этом занятии нам понадобятся следующие три теоремы.
Теорема 1 (соотношение между сторонами и углами треугольника). В любом треугольнике против большего угла лежит бóльшая сторона, и наоборот.
Теорема 2 (неравенство треугольника). Если А, В, С — вершины треугольника, то выполнено неравенство АВ + ВС > AC.
Теорема 3 (обобщенное неравенство треугольника). Если А, В, С — три точки на плоскости (или в пространстве), то выполнено неравенство АВ + ВС ≥ AC. При этом равенство достигается тогда и только тогда, когда эти три точки лежат на одной прямой, причем точка В лежит между точками А и С.
- 1.
-
Юля говорит, что для любых трех точек A, B, и C на плоскости верно неравенство: АВ ≥ |АС − ВС|.
Докажите, что она права.
Решение. В зависимости от того, какой знак имеет выражение |АС − ВС|, доказываемое неравенство равносильно либо неравенству АВ ≥ АС − ВС, либо неравенству АВ ≥ ВС − АС. Перенося в первом неравенстве ВС в левую часть (а во втором, соответственно, перенося в левую часть АС), получим неравенство АВ + ВС ≥ АС (или, соответственно, АВ + АС ≥ ВС). Оба эти неравенства — это неравенства треугольника, получающиеся из треугольника АВС.
- 2.
-
Света утверждает, что в треугольнике длина любой его стороны не превосходит полупериметра. Докажите, что Света не
ошибается.
Решение. Пусть стороны треугольника имеют длины a, b, c, тогда его полупериметр равен ½(a + b + c). Докажем, например, что a ≤ ½(a + b + c). Умножив обе части этого неравенства на 2, получим неравенство 2a ≤ a + b + c. Перенося а из правой части в левую, получим a ≤ b + c. А это и есть неравенство треугольника. Точно так же это утверждение можно доказать и для других сторон.
- 3.
-
Поля думает, что длина любой диагонали четырёхугольника меньше половины его периметра. Не ошибается ли она?
Ответ обоснуйте.
Ответ. Не ошибается.Решение.
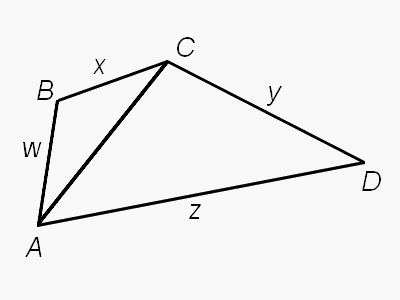 Обозначим длины сторон четырехугольника ABCD через w, x, y, z,
а длину диагонали АС обозначим d (см. рисунок).
Запишем неравенство треугольника для треугольника АВС, заменяя АВ на w, ВС на х и
АС на d. Получится w + x > d.
Теперь то же самое проделаем для треугольника ACD. Получим y + z > d.
Сложив эти два неравенства,
получим w + x + y + z > 2d.
Поделив обе части неравенства на 2, получим
½(w + x + y + z) > d.
В левой части
этого неравенства стоит половина периметра четырехугольника, а в правой — длина диагонали. Тем самым
утверждение Поли доказано.
Обозначим длины сторон четырехугольника ABCD через w, x, y, z,
а длину диагонали АС обозначим d (см. рисунок).
Запишем неравенство треугольника для треугольника АВС, заменяя АВ на w, ВС на х и
АС на d. Получится w + x > d.
Теперь то же самое проделаем для треугольника ACD. Получим y + z > d.
Сложив эти два неравенства,
получим w + x + y + z > 2d.
Поделив обе части неравенства на 2, получим
½(w + x + y + z) > d.
В левой части
этого неравенства стоит половина периметра четырехугольника, а в правой — длина диагонали. Тем самым
утверждение Поли доказано.
Замечание. Обратите внимание, что такое же доказательство годится и для обеих диагоналей невыпуклого четырехугольника, у которого одна из диагоналей лежит внутри, а другая снаружи четырехугольника. Нарисуйте чертеж для этого случая и убедитесь в этом самостоятельно.
- 4.
-
Даша уверена, что если ABCD — выпуклый четырёхугольник, то AB + CD < AC + BD. Права ли она?
Ответ. Права.Решение.
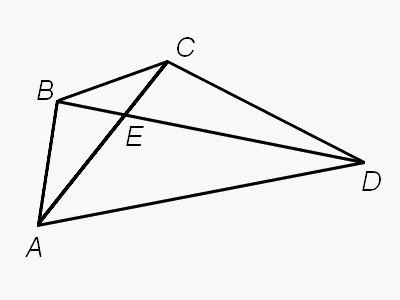 Обе диагонали выпуклого четырехугольника ABCD лежат внутри него, а значит, пересекаются в некоторой точке Е
(убедитесь, что параллельными они быть не могут). Запишем неравенства треугольника для треугольников АВЕ и CDE:
Обе диагонали выпуклого четырехугольника ABCD лежат внутри него, а значит, пересекаются в некоторой точке Е
(убедитесь, что параллельными они быть не могут). Запишем неравенства треугольника для треугольников АВЕ и CDE:
AB < AE + BE;
CD < CE + DE.
Сложив эти два неравенства, получим: AB + CD < (AE + CE) + (BE + DE). Заметим, что правая часть этого неравенства равна AC + BD. Поэтому получим AB + CD < AC + BD, что и требовалось доказать. - 5.
-
Света считает, что если ABCD — выпуклый четырёхугольник, причём AB + BD ≤ AC + CD, то AB < AC.
Верно ли это?
Ответ. Верно.Решение. Вспомним неравенство, доказанное нами в предыдущей задаче: AB + CD < AC + BD (напомним, оно верно для всякого выпуклого четырехугольника ABCD). Теперь сложим его с неравенством, данным в условии этой задачи. Получим 2AB + BD + CD ≤ 2AC + BD + CD. Вычитая из обеих частей этого неравенства (BD + CD), получим 2AB < 2AC. Поделив обе части этого неравенства пополам, получим требуемое неравенство.
- 6.
-
У Насти расстояние от дома до магазина 200 м, от магазина до парикмахерской 300 м,
от парикмахерской до школы 500 м, а от дома до школы 1 км. Какое расстояние от дома Насти до
парикмахерской?
Ответ. 500 м.Решение.
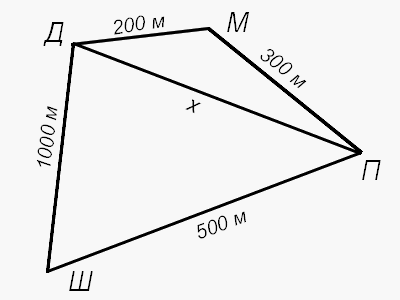 Обозначим упомянутые в условии места буквами Д, М, П и Ш соответственно. Обозначим искомое расстояние от дома
Насти до парикмахерской за x. Запишем неравенство треугольника для треугольника ДМП:
ДП ≤ ДМ + МП, или x ≤ 200 + 300 = 500. Теперь запишем неравенство треугольника для треугольника
ДШП: ДШ ≤ ДП + ШП, или 1000 ≤ x + 500, откуда x ≥ 500. Сопоставляя полученные
неравенства, заключаем, что x = 500.
Обозначим упомянутые в условии места буквами Д, М, П и Ш соответственно. Обозначим искомое расстояние от дома
Насти до парикмахерской за x. Запишем неравенство треугольника для треугольника ДМП:
ДП ≤ ДМ + МП, или x ≤ 200 + 300 = 500. Теперь запишем неравенство треугольника для треугольника
ДШП: ДШ ≤ ДП + ШП, или 1000 ≤ x + 500, откуда x ≥ 500. Сопоставляя полученные
неравенства, заключаем, что x = 500.
Замечание 1. В неравенствах треугольника, использованных в этой задаче, стоят знаки ≤ и ≥, а не < и >. Это связано с тем, что Д, М, П и Ш — уже не обязательно вершины каких-то треугольников (как это было в предыдущих задачах), а произвольные точки на плоскости. Из полученного ответа, в частности, следует, что эти точки на самом деле лежат на одной прямой (подумайте, в каком порядке).
Замечание 2. Хотя в итоге оказалось, что все четыре точки лежат на одной прямой, с самого начала этого предполагать было нельзя. То есть неверно было бы сразу делать вывод, что искомое расстояние равно 200 + 300 = 500 м.
- 7.
-
Юля нарисовала треугольник АВС,в котором серединный перпендикуляр к стороне ВС пересекает сторону АВ
в точке D и продолжение стороны АС в точке Е. Докажите, что AD < AE.
Решение.
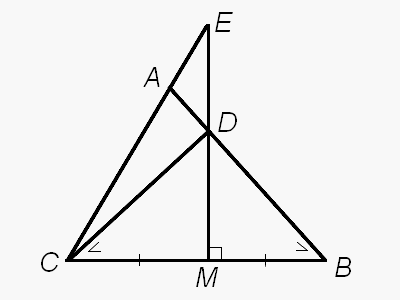 Проведем дополнительно отрезок CD. Заметим, что ΔBCD — равнобедренный, так как точка D лежат на
серединном перпендикуляре к отрезку ВС и значит, равноудалена от его концов (это основное свойство серединного
перпендикуляра к отрезку). Следовательно, ∠BCD = ∠CBD как углы при основании равнобедренного треугольника.
А поскольку ∠ACB = ∠BCD + ∠DCE, заключаем, что ∠ACB > ∠CBD.
Проведем дополнительно отрезок CD. Заметим, что ΔBCD — равнобедренный, так как точка D лежат на
серединном перпендикуляре к отрезку ВС и значит, равноудалена от его концов (это основное свойство серединного
перпендикуляра к отрезку). Следовательно, ∠BCD = ∠CBD как углы при основании равнобедренного треугольника.
А поскольку ∠ACB = ∠BCD + ∠DCE, заключаем, что ∠ACB > ∠CBD.
По теореме о сумме углов трегольника для прямоугольного ΔCME получаем, что ∠CEM + ∠BCE = 90°; аналогично из ΔBMD находим, что ∠CBD + ∠BDM = 90°. Значит, ∠BDM = 90° - ∠CBD и ∠CEM = 90° - ∠BCE. Вместе с полученным выше неравенством это дает, что ∠BDM > ∠CEM.
Теперь рассмотрим треугольник ADE. В нем ∠AED = ∠CEM (это просто два разных обозначения одного и того же угла), ∠ADE=∠BDM как вертикальные углы. Тогда из полученного выше неравенства делаем вывод, что ∠AED < ∠ADE. Но в треугольнике против большего угла лежит бóльшая сторона, поэтому AD < AE, что и требовалось доказать.
- 8.
-
Дом Поли недалеко от реки. В сарае (с той же стороны реки) живут козы. Коз нужно поить водой из реки три раза в
день. Носить воду от реки Поле помогает ее друг Гриша. Но Гриша очень ленивый, поэтому ему хочется,
чтобы расстояние, которое он будет проходить от дома до сарая, было минимальным. В каком месте реки ему надо
набирать воду (берег реки — прямая)?
Примечание.
В первоначальной версии (которая и предлагалась на занятии) эта задача выглядела так:
Дом Поли недалеко от реки. В сарае (с той же стороны реки) живут козы. В каком месте реки ей нужно набирать воду, чтобы поить коз? Поле хочется, чтобы расстояние, которое она будет проходить от дома до сарая, было минимальным (берег реки — прямая).
Составитель решений, в отличие от составителя задач, пожалел Полю и придумал ей помощника Гришу (ну в самом деле, зачем девочке самой таскать тяжелые ведра с водой?). Кстати: все совпадения с реальными людьми, козами и событиями являются случайными!
Решение.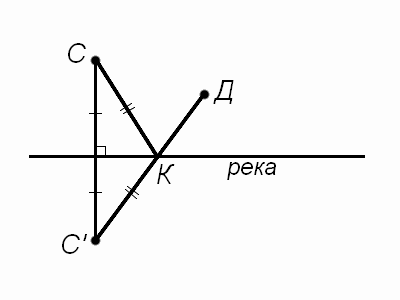 Избразим «план местности», обозначив дом Поли Д, а сарай С (см. чертеж). Отметим на этом чертеже
точку С', симметричную точке С относительно берега реки (то есть такую, что берег реки является серединным
перпендикуляром к отрезку CC').
Избразим «план местности», обозначив дом Поли Д, а сарай С (см. чертеж). Отметим на этом чертеже
точку С', симметричную точке С относительно берега реки (то есть такую, что берег реки является серединным
перпендикуляром к отрезку CC').
Выберем какую-нибудь точку К на берегу реки. Заметим, что СК = C'K по свойству серединного перпендикуляра к отрезку. Поэтому длина маршрута ДКС от дома до сарая с набором воды в точке К равна длине ломаной ДКС'. Тем самым надо выбрать такую точку К, чтобы длина этой ломаной была минимальна. А для этого ломаная должна быть отрезком прямой. То есть точка К строится как точка пересечения прямой ДС' и берега реки.
Замечание. Если у Поли и Гриши есть план местности (или хотя бы возможность его составить), то указанные построения они могут провести на этом плане, а потом найти соответствующую точку К на местности. А вот если план составить не представляется возможным, то на практике задачу решить ребятам будет трудно даже вдвоем. Ведь построить точку C'(которая может оказаться на другом берегу реки или в самой реке) в этом случае не получится. Попробуйте пофантазировать и помогите Поле и Грише справиться с этой задачей.
- 9.
-
Полуостров представляет собой острый угол, внутри которого находится дом Светы. Как Свете, выйдя из дома,
добраться сначала до одного берега полуострова, затем до другого и вернуться домой, пройдя при этом по самому
короткому пути?
Решение.
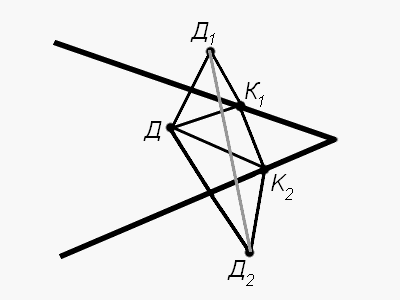 Будем решать эту задачу аналогично предыдущей. Обозначим на плане дом Светы Д и построим точки Д1 и
Д2,
симметричные ей относительно берегов полуострова (см. чертеж). Выберем какие-нибудь точки К1 и К2
на берегах
полуострова. Аналогично предыдущей задаче сообразим, что длина маршрута ДК1К2Д равна
длине ломаной
Д1К1К2Д2.
Чтобы эта длина была минимальной, нужно, чтобы ломаная была отрезком прямой. Для этого точки К1
и К2
построим как точки пересечения прямой Д1Д2 и соответствующих берегов реки.
Будем решать эту задачу аналогично предыдущей. Обозначим на плане дом Светы Д и построим точки Д1 и
Д2,
симметричные ей относительно берегов полуострова (см. чертеж). Выберем какие-нибудь точки К1 и К2
на берегах
полуострова. Аналогично предыдущей задаче сообразим, что длина маршрута ДК1К2Д равна
длине ломаной
Д1К1К2Д2.
Чтобы эта длина была минимальной, нужно, чтобы ломаная была отрезком прямой. Для этого точки К1
и К2
построим как точки пересечения прямой Д1Д2 и соответствующих берегов реки.
- 10.
-
Юля утверждает, что в любом треугольнике сумма медиан больше 3/4 периметра, но меньше периметра.
Докажите, что она права.
Примечание.
Для решения этой задачи нам понадобится следующий факт.
Теорема о пересечении медиан треугольника.
Все три медианы любого треугольника пересекаются в одной точке и этой точкой делятся в отношении 2 к 1, считая от вершины.
То есть отрезок любой медианы от вершины треугольника до точки пересечения медиан в два раза длиннее, чем отрезок этой же медианы от точки пересечения медиан до точки ее пересечения со стороной треугольника.Вполне вероятно, что вы еще не изучали ее в школе. В этом случае разберитесь в приведенном решении, считая теорему верной (хотя доказательство вам пока и неизвестно). После решения этой задачи приведено доказательство аналогичного, но более слабого утверждения, доказательство которого не требует применения этой теоремы.
Решение.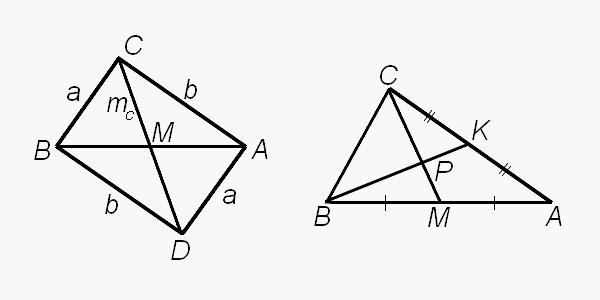
Назовем наш треугольник АВС. Обозначим длины сторон этого треугольника a, b, c, а длины медиан, проведенные к соответствующим сторонам, через ma, mb, mc. Достроим треугольник до параллелограма так, как показано на чертеже. Для этого через вершину А проведем прямую, параллельную прямой ВС, а через вершину В — прямую, параллельную АС. Точку пересечения построенных прямых обозначим D. ACBD — параллелограм по построению.
Обозначим точку пересечения медианы, проведенной из вершины С к стороне АВ, с этой стороной через М. Продолжим прямую СМ за точку М. Эта прямая пройдет и через точку D. Вспомним, что диагонали параллелограма точкой пересечения делятся пополам. Значит, если прямая проходит через одну из вершин паралелограма и середину диагонали, не проходящей через эту же вершину, то эта прямая является второй диагональю параллелограма и в частности, проходит и через противоположную вершину параллелограма.
Итак, у нас есть параллелограм ACBD с длинами сторон a и b. Длины его диагоналей равны с и 2mc. Запишем неравенство треугольника для ΔBCD: 2mc < a + b, откуда mc < (a + b)/2. Аналогично доказываются неравенства ma < (b + c)/2 и mb < (a + c)/2. Сложив эти три неравенства, получим ma + mb + mc < a + b + c. Тем самым доказано второе утверждение задачи.
Докажем первое утверждение задачи. Проведем из вершины В медиану ВК и обозначим точку ее пересечения с медианой СМ через Р. По теореме о пересечении медиан треугольника (см. примечание к этой задаче) СР:РМ = 2:1; кроме того, СР + РМ = СМ = mc. Следовательно, СР = (2/3)·mc. Аналогично доказывается, что BP = (2/3)·mb.
Запишем неравенство треугольника для ΔВСР: BP + CP > BC, то есть
(2/3)·mb + (2/3)·mc > a, откуда mb + mc > (3/2)·a.
Аналогично получим неравенства
ma + mb > (3/2)·c,
ma + mc > (3/2)·b.
Теперь, складывая эти неравенства, получим 2·(ma + mb + mc) > (3/2)·(a + b + c), откуда ma + mb + mc > (3/4)·(a + b + c), что и требовалось доказать.Дополнение. Без использования теоремы о пересечении медиан треугольника можно доказать, что сумма длин медиан треугольника больше его полупериметра. Вспомним обозначения, которыми мы пользовались при доказательстве второго утверждения нашей задачи. Запишем, например, неравенство треугольника для ΔBCM: BC < BM + MC, или a < mc + c/2.
Аналогично получаются неравенства
b < mc + c/2,
a < mb + b/2,
c < mb + b/2,
b < ma + a/2,
c < ma + a/2.
Сложив эти неравенства, получим
2·(a + b + c) < 2·(ma + mb + mc) + a + b + c,
откуда получаем ma + mb + mc > ½·(a + b + c). - 11.
-
Настя нарисовала на плоскости квадрат ABCD и произвольную точку О. Докажите, что АО + ВО + СО > DO.
Решение. Запишем неравенство треугольника для ΔBOD и ΔAOC (это могут быть и не настоящие трегольники, а просто тройки точек на плоскости, поэтому неравенства нестрогие):
DO ≤ BO + BD;
AC ≤ AO + CO.
Так как ABCD — квадрат, BD = AC. Тогда при помощи этого факта и неравенств получим, что:
DO ≤ BO + BD = BO + AC ≤ BO + AO + CO.
Это неравенство нестрогое, а нам нужно доказать аналогичное ему строгое. Заметим, однако, что равенство в нестрогих неравенствах треугольника достигается лишь тогда, когда соответствующие три точки лежат на одной прямой. То есть одновременно в обоих неравенствах оно достигается лишь тогда, когда точка О лежит на прямых AC и BD одновременно (проверьте!). Тогда эта точка будет просто точкой пересечения диагоналей квадрата ABCD, и требуемое неравенство очевидно. Во всех остальных случаях хотя бы одно из этих неравенств будет строгим. Тогда из наших рассуждений будет следовать, что DO < AO + BO + CO.