МАЛЫЙ МЕХМАТ МГУ
Кружок 8 класса
2010/2011 учебный год
Занятие 1. Письменная работа
- 1.
-
Верно ли, что
для любого действительного числа х, отличного от 0? Ответ обоснуйте.1 + 1 ≥ 2 x² x Ответ. Верно.Решение. Перенеся все слагаемые в левую часть неравенства, получим
Заметим, что выражение в левой части неравенства можно преобразовать по формуле сокращенного умножения:1 + 1 - 2 ≥ 0 x² x
Это выражение имеет смысл и неотрицательно при всех x≠0 и, стало быть, при всех таких x неравенство верно.1 + 1 - 2 = 1- 2 + 1 = 1-2· ( 1 )+ ( 1 )²= ( 1- 1 )² x² x x x² x x x - 2.
-
Улитка ползет по столбу вверх. За день она поднимается на 5 см вверх, а за ночь,
уснув, случайно сползает на 3 см. Высота столба 1 м. На какой день улитка
доползет до его вершины?
Ответ. На сорок девятый день.Решение. За одни сутки (то есть за день и следующую за ним ночь) улитка в общей сложности продвигается на 2 см вверх по столбу. Однако неверно было бы считать, что она доползет до вершины столба за 100:2=50 дней. Заметим, что через 48 суток улитка окажется на высоте 48×2=96 см. Соответственно, в конце сорок восьмого дня (а не сорок восьмых суток!) она будет находиться на высоте 96+2=98 см, то есть еще не достигнет вершины столба. Но утром следующего, сорок девятого дня, она стартует на высоте 96 см, и ей достаточно будет подняться всего на 4 см, чтобы оказаться на вершине столба в тот же (сорок девятый) день. После этого уже не имеет значения то, что за следующую ночь она должна была бы сползти на 3 см вниз. Такой эффект возникает из-за разницы между тем, что происходит с улиткой за один день и тем, что происходит с ней за одни сутки.
- 3.
-
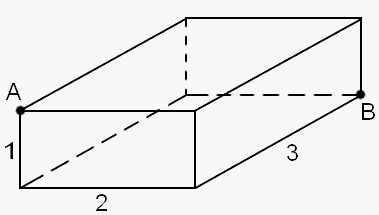Дан прямоугольный параллелепипед со сторонами 1 см, 2 см и 3 см (см. рисунок).
Муха, сидящая в точке А, хочет кратчайшим путем доползти до точки
В по граням параллелепипеда. Как ей это сделать и какой путь она при
этом проползет?
Подсказка. Нарисуйте развертку.Решение.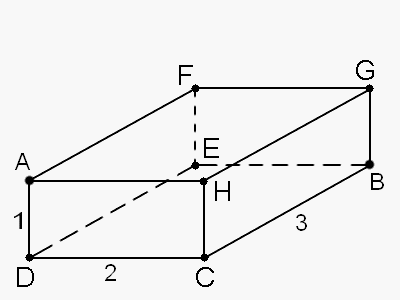
Для удобства обозначим остальные вершины параллелепипеда буквами, как показано на первом рисунке. Теперь нарисуем развертку параллелепипеда. Для этого нужно «разрезать» параллелепипед по ребрам AD, CH, EF, BG, AH, AF, GH и «развернуть» на плоскость. В результате на плоскости получится фигура, изображенная на втором рисунке.
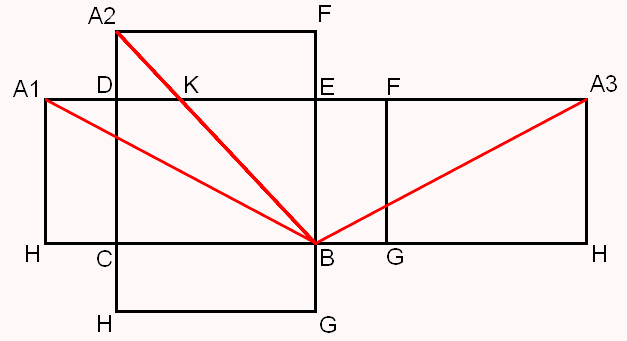
Обратите внимание, что одной и той же вершине исходного параллелепипеда могут соответствовать несколько различных точек на развертке. Например,вершине А соответствуют три точки A1, A2, A3. (Остальные такие вершины найдите на чертеже самостоятельно). То же самое относится и к ребрам. При работе с разверткой об этой особенности нельзя забывать. Зато на развертке проще искать кратчайший путь между двумя точками: здесь этот путь, как и обычно на плоскости, проходит по прямой. Этим мы и воспользуемся.
На нашей развертке есть три «кратчайших» пути между точками A и B: вдоль отрезков A1B, A2B и A3B. Осталось выбрать из этих отрезков самый короткий; он и будет соответствовать кратчайшему пути между точками A и B на исходном параллелепипеде. Чтобы получить его изображение на поверхности параллелепипеда, надо снова «склеить» параллелепипед из развертки с нарисованной на ней оптимальной траекторией движения мухи.
Заметим сначала, что отрезки A1B и A3B имеют равную длину (убедитесь в этом самостоятельно, используя признаки равенства треугольников). Теперь вычислим длины отрезков A1B и A2B с помощью теоремы Пифагора: в прямоугольном треугольнике сумма квадратов длин катетов (сторон, лежащих против острых углов) равна квадрату длины гипотенузы (стороны, лежащей против прямого угла). (Если вы еще не изучали ее в школе, найдите ее доказательство в учебнике геометрии или где-нибудь еще). Применив эту теорему к прямоугольным треугольникам A1BH и A2BC, получим соотношения $(A1B)² = (A1H)² + (BH)² = (A1H)² + (BC + CH)² = 2² + 4² = 20$ и $(A2B)² = (A2С)² + (BС)² = (A2D + DC)² + (BC)² = 3² + 3² = 18$. Отсюда найдем, что A1B = √20 > A2B = √18. (По определению, квадратный корень из неотрицательного числа a (обозначается √a) — это такое неотрицательное число b, что b² = a.) Таким образом, кратчайший путь между точками A и B на поверхности параллелепипеда соответствует отрезку A2B на развертке, а длина его равна √18. Докажите самостоятельно, что, двигаясь по этому маршруту, муха будет переползать с грани ADEF на грань BCDE в точке K, находящейся на расстоянии 1 от точки D (делать это тоже удобнее с использованием развертки).
- 4.
-
Есть две кучи камней: в первой куче 2009 камней, а во второй — 2010.
Света и Даша играют в такую игру: за один ход каждая девочка берет камни из
одной кучи, причем не более ста. Проигрывает тот, кто не может сделать хода.
Первый ход делает Даша. Кто выигрывает при правильной игре?
Ответ. Выигрывает Даша.Решение. Первым ходом Даша должна взять один камень из кучи, где камней первоначально 2010. После этого две кучи станут совершенно одинаковыми. Далее, если Света своим очередным ходом берет k камней из какой-либо кучи, Даша должна своим следующим ходом взять k камней из другой кучи. При такой стратегии после каждого хода Даши в обеих кучах будет оставаться равное число камней, а после хода Светы — неравное. Поэтому после очередного хода Светы камни в обеих кучах не могут закончиться, и значит, Даша не проиграет.
- 5.
-
В городе Маленький 15 телефонов. Можно ли их соединить проводами так, чтобы
каждый телефон был соединен ровно с пятью другими?
Ответ. Нельзя.Решение. Решим эту задачу методом «от противного». Предположим, что соединить телефоны указанным образом удалось, и попытаемся сосчитать количество проводов, которое для этого потребовалось. К каждому из 15 телефонов подключено по пять проводов, и можно было бы подумать,что всего проводов 15·5=75. На самом деле это не так: каждый провод мы сосчитали два раза (по одному разу для каждого из двух телефонов, которые он соединяет). Значит, проводов должно быть в два раза меньше, то есть 75:2. Но 75 — число нечетное, поэтому число 75:2 будет дробным. А количество проводов по понятным причинам может быть только целым. Полученное противоречие доказывает, что наше предположение ошибочно. Стало быть, соединить телефоны указанным образом невозможно.
- 6.
-
ABCD — четырехугольник, причем AD ∥ BC,
AM ⊥ BD, AM — биссектриса угла BAD,
∠BMA = ∠ABD. Доказать, что ABMD — квадрат.
Решение.
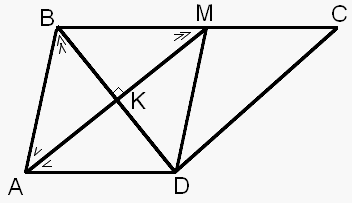
1. ∠DAM = ∠AMB как накрест лежащие углы при параллельных прямых AD ∥ BC и секущей AM. Значит, ∠DAM = ∠AMB = ∠ABD = ∠BAM.
2. Обозначим AM∩BD = K (символ ∩ означает пересечение). Из прямоугольного (по условию) ΔABK по теореме о сумме углов треугольника и с учетом п. 1 получаем ∠BAK = ∠ABK = ½·(180°-∠AKB) = 45°. Отсюда (или сразу из п. 1) следует, что ΔABK — равнобедренный.
3. С помощью признаков равенства треугольников получаем, что ΔABK = ΔBKM = ΔMKD = ΔAKD (убедитесь в этом самостоятельно). Из равенства этих треугольников следует равенство их острых углов (они все равны 45°). Отсюда получаем, что все углы четырехугольника ABMD — прямые. Кроме того, из равенства тех же треугольников следует равенство их гипотенуз (сторон, лежащих против прямых углов), а они служат сторонами четырехугольника ABMD. Таким образом, ABMD — прямоугольник, у которого все стороны равны, то есть квадрат, что и требовалось доказать.
- 7.
-
Поля, Даша, Света и Юля были на математической олимпиаде. В ответ на вопрос
«Кто из вас решил последнюю задачу?» каждая девочка высказала два
утверждения:
Поля: «Даша не решила задачу. Я тоже ее не решила».
Даша: «Юля решила задачу. А вот Света — нет».
Света: «Да, задачу решила Юля. А вот я не смогла».
Юля: «Поля решила задачу. Света — тоже».
Кто мог решить задачу, если каждая девочка один раз сказала правду, а один раз ошиблась? Перечислите все возможные случаи: задачу могли решить и несколько девочек.Ответ. Задачу могла решить либо только Поля, либо все, кроме Поли.Решение.Обратим внимание, что Света и Даша утверждают одно и то же, хотя и в разной последовательности. Это означает, что одинаковые их утверждения либо одновременно истинны, либо одновременно ложны. В зависимости от того, какая пара (одинаковых) утверждений истинна, а какая ложна, возможны два различных случая. Рассмотрим их по отдельности.
Случай 1. Пусть утверждение о том, что Света не решила задачу, истинно, а утверждение о том, что ее решила Юля, ложно. Тогда второе утверждение Юли ложно, а ее первое утверждение истинно. Значит, второе утверждение Поли ложно, а первое — истинно. Окончательно получается, что в этом случае задачу решила только одна девочка, а именно Поля.
Случай 2. Пусть теперь истинно утверждение о том, что Юля решила задачу, а второе утверждение Светы и Даши ложно. Эта ситуация полностью противоположна рассмотренной выше (убедитесь в этом сами). Значит, в этом случае задачу решили три девочки: Света, Даша и Юля.
- 8.
-
Для каких простых чисел p число p+1 также является простым?
Ответ. Только для p=2.Решение.
Во-первых, заметим, что числа p и p+1 имеют разную четность (то есть если одно из них четно, другое обязательно будет нечетным, и наоборот). Во-вторых, обратим внимание, что среди простых чисел есть только одно четное, а именно число 2 (подумайте почему). Значит, одно из чисел p и p+1 должно быть равно 2.
Если p=2, то p+1=3, и оба эти числа являются простыми. Если же p+1=2, то p=1, а единица простым числом не считается. Поэтому единственное значение p, которое нас устраивает, — значение p=2.
