
МАЛЫЙ МЕХМАТ МГУ

Кружок 8 класса
2010/2011 учебный год
Занятие 15. Письменная работа
- 1.
-
У Васи есть чашечные весы и 9 гирь с массами 1 кг, 2 кг, 3 кг, …, 9 кг. Вначале
он ставит одну из гирь на любую чашку весов, а затем на каждом шаге ставит на
более лёгкую чашку любую из оставшихся гирь, но так, чтобы весы при этом не
оказались в равновесии. На какое наибольшее число килограммов одна чашка весов
могет перевешивать другую после того, как будут выставлены все 9 гирь?
Ответ. На 7 кг.Решение.
Сначала докажем, что число килограммов, на которое одна чашка весов может перевешивать другую, не превосходит 7. Общий вес всех гирь равен 45 кг. Пусть общий вес гирь на более легкой чаше весов в конце концов оказывается равным x кг, а на более тяжелой x + d кг (d > 0). Тогда суммарный вес гирь равен x + (x + d) = 2x + d = 45. Из этого следует, что число d всегда нечетно и, в частности, не может быть равным 0; для нас, однако, важнее то, что оно не может быть равным 8.
Предположим, что перевес одной из чашек оказался равным 9 кг или больше. Попробуем определить, куда была поставлена последняя гиря. На более тяжелую чашку последняя гиря поставлена быть не могла. Ведь если бы это была гиря массой 9 кг, то на предыдущем шаге весы были бы или в равновесии, чего быть не могло, либо эта чашка уже была более тяжелой на предыдущем шаге, и на нее по правилам нельзя было бы ставить гирю. Если же последняя гиря была легче 9 кг, то до ее установки на весы чашка, куда ее поставили, уже была бы более тяжелой, и ставить на нее гирю было бы уже нельзя. Таким образом, последняя гиря была поставлена на более легкую чашку. Но это означает, что на предыдущем шаге перевес более тяжелой чашки был также не меньше 9 кг, и по аналогичным соображениям вторая с конца гиря тоже была поставлена на более легкую чашку, и так далее. В итоге получается, что все гири ставились на одну и ту же чашку (которая в итоге оказалась более легкой), чего быть не могло. Поэтому и перевес одной из чашек не может оказаться больше 8 кг. В силу сделанного выше замечания он не может быть равен и 8 кг, поэтому максимально возможное его значение равно 7 кг.
Теперь приведем пример последовательной расстановки гирь согласно условию, дающей в итоге перевес одной чашки на 7 кг (вы можете придумать и свои собственные примеры). Если общий вес гирь на одной из чашек весов (например, на более легкой), равен x кг, то общий вес гирь на второй чашке должен быть равен (x + 7) кг. Из условия x + (x + 7) = 45 найдем, что x = 19 кг. Например, гири весом 1 кг, 2 кг, 3 кг, 4 кг и 9 кг вместе весят как раз 19 кг. Осталось придумать способ последовательной расстановки гирь в соответствии с условием задачи, при котором эти пять гирь в конце концов оказались бы на одной чашке весов, а оставшиеся четыре — на другой. Соответствующий пример приведен в таблице ниже. Там последовательно перечислены наборы гирь, которые оказываются на каждой из чаш весов на очередном шаге. «Только что добавленная» гиря выделяется курсивом. Убедитесь, что на каждом шаге очередная гиря действительно ставится на более легкую чашку и что весы ни разу не оказались в равновесии.
9 - 9 5 9 5, 6 1, 9 5, 6 1, 2, 9 5, 6 1, 2, 9 5, 6, 7 1, 2, 3, 9 5, 6, 7 1, 2, 3, 4, 9 5, 6, 7 1, 2, 3, 4, 9 5, 6, 7, 8 Упражнение. При решении этой задачи мы фактически показали, что одна чашка весов может оказаться тяжелее другой только на 1 кг, 3 кг, 5 кг или 7 кг. Придумайте, как и в какой последовательности расставить гири, чтобы получить перевес в 1 кг, 3 кг и 5 кг.
- 2.
-
В парламенте одной страны 8 депутатов. Известно, что среди любых трех депутатов
есть хотя бы один нечестный. Укажите наибольшее возможное число честных
депутатов в этом парламенте.
Ответ. Два.Решение. Если бы в парламенте было хотя бы трое честных депутатов, то среди этих трех не было бы нечестных, что противоречит условию. Значит, честных депутатов в этом парламенте не больше двух. В частности, если честных депутатов двое, условие задачи выполнено.
- 3.
-
Из множества чисел
{√15/4,
√18/5,
√9/2,
√11/3}
выберите наименьшее.
Ответ. √18/5.Решение.
Арифметический квадратный корень — монотонно возрастающая функция. Поэтому если выбрать наименьшее из чисел, стоящих под знаками корня, то корень из него будет наименьшим из наших четырех чисел.
Приведя все дроби к общему знаменателю 60, получим, соответственно, 225/60, 216/60, 270/60 и 220/60. Из этих чисел наименьшим, очевидно, является число 216/60. Значит, из исходных четырех чисел наименьшим является число √18/5.
- 4.
-
Укажите значение Δ, при котором выполняется равенство
8Δ = 128 · 4Δ.
Ответ. Δ = 7.Решение.
Перепишем равенство в виде (23)Δ = 27·(22)Δ, то есть 23Δ = 27·22Δ, или 23Δ = 27 + 2Δ, откуда 3Δ = 7 + 2Δ, то есть Δ = 7.
Замечание. Утверждение «если 2x = 2y, то x = y», которым мы воспользовались при решении этой задачи, верно, но отнюдь не является очевидным. Его строгое обоснование дается обычно в школьном или университетском курсе математического анализа. Поэтому при его использовании пока что лучше проверять полученный результат подстановкой. Проверьте самостоятельно, что найденное нами при решении задачи значение Δ = 7 действительно удовлетворяет исходному равенству. Проделайте вычисления без использования калькулятора!
- 5.
-
Даны три прямых угла с вершиной в одной точке. Первый со вторым имеют общий
угол, равный 45°, а второй с третьим имеют общий угол, равный 60°. Чему
может быть равна их общая часть?
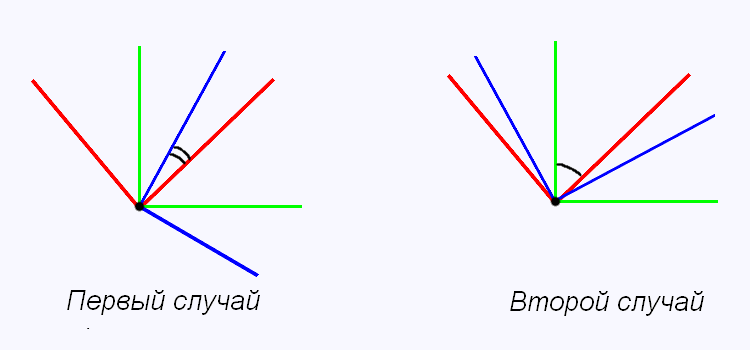
Ответ. 15° или 45°.Пояснение. Есть два принципиально разных случая расположения углов, удовлетворяющих условию задачи (см. рисунок). Первый угол в обоих случаях изображен красным цветом, второй — зеленым и третий — синим. Общие части трех углов (это пересечение, а не объединение их внутренностей!) выделены дугами. Несложно подсчитать, что в первом случае общая часть трех углов равна 15°, а во втором случае — 45°. Все остальные возможные случаи совпадают с указанными с точностью до симметрий и поворотов.
- 6.
-
Какая первая цифра в наименьшем натуральном числе, сумма цифр которого равна 2011?
Ответ. 4.Решение. Чтобы составить число из минимально возможного количества цифр, надо как можно больше цифр сделать девятками, а остаток от деления нужной суммы цифр на 9 взять в качестве еще одной цифры (если этот остаток равен 0, то эта последняя цифра вовсе не нужна). 2011 = 2007 + 4 = 9·223 + 4. Значит, если составить число из 223 девяток и одной четверки, сумма его цифр будет как раз равна 2011. Число с такой же суммой цифр нельзя составить из меньшего количества цифр (докажите это аккуратно). А чем меньше цифр в записи натурального числа, тем меньше само это число. Поэтому наименьшее число с суммой цифр 2011 надо искать среди тех из них, десятичная запись которых состоит из 224 цифр. Ясно, что цифр меньше 4 в таких числах не будет. Более того, и четверка там может быть только одна. Эту одну четверку мы и поставим в старший разряд, а на оставшихся местах тогда окажутся девятки. Такое число и будет наименьшим натуральным числом с суммой цифр 2011.
- 7.
-
На гипотенузе АВ прямоугольного треугольника АВС отмечены точки Е и D, причём
ЕА = АС, а DB = ВС. Найдите ∠DCE.
Ответ. 45°.Решение.
В силу неравенства треугольника и условия задачи AB < AC + BC = AE + BD, поэтому точки на прямой АВ расположены в следующем порядке: A, D, E, B. Этот факт нам в дальнейшем пригодится.
Пусть ∠A = α. По условию ΔACE — равнобедренный, поэтому ∠ACE = ∠AEC. А поскольку сумма углов треугольника равна 180°, отсюда находим, что ∠AEC = ∠ACE = (180° - α)/2 (проверьте!). Аналогично, обозначив ∠B = β, из равнобедренного ΔBCD найдем, что ∠BCD = ∠BDC = (180° - β)/2.
Теперь рассмотрим ΔCDE. В нем ∠CED = (180° - α)/2, ∠CDE = (180° - β)/2 (здесь-то нам и пригодилось замечание, сделанное в самом начале решения: ∠CED = ∠BCD, а не ∠ADC!). По теореме о сумме углов треугольника ∠DCE = 180° - ∠CED - ∠CDE = 180° - (180° - α)/2 - (180° - β)/2 = (α + β)/2. Вспоминая, что α = ∠A, β = ∠B, из исходного ΔABC найдем α + β = 180° - ∠ACB = 90°, поэтому ∠DCE = (α + β)/2 = 45°.
- 8.
-
Известно, что
Найдите значение выраженияx - y = 5. y 3x - 2y 2x/3 Ответ. 4.Решение.Вспомнм, что дробь — это запись результата деления ее числителя на ее знаменатель (если, конечно, этот знаменатель не равен нулю). Нам известно, что (x - y)/y = 5, то есть
x/y - y/y = 5,
x/y - 1 = 5,
или x/y = 6.Прежде чем вычислять значение второго выражения, объясним, почему оно имеет смысл (то есть почему знаменатель дроби не равен нулю в условиях задачи). Если бы знаменатель второй дроби был равен нулю, то x = 0. Подставив это значение в равенство из условия задачи, получим -y/y = 5, что, очевидно, не выполняется ни для какого y ≠ 0, а при y = 0 не имеет смысла. Полученное противоречие показывает, что на самом деле в условиях задачи x ≠ 0, поэтому второе выражение имеет смысл.
Теперь упростим второе выражение так же, как выше упростили первое: (3x - 2y)/((2/3)x) = 3x/((2/3)x) - 2y/((2/3)x) = 9/2 - 3y/x.
Из того, что x/y = 6, найдем y/x = 1/(x/y) = 1/6. Поэтому (3x - 2y)/((2/3)x) = 9/2 - 3y/x = 9/2 - 3·(1/6) = 4.