МАЛЫЙ МЕХМАТ МГУ

Кружок 8 класса

Занятие 25. Разнобой

1.

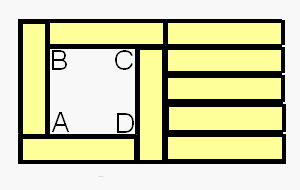
Из девяти одинаковых брусков составлена конструкция (см. рисунок). Найти площадь одного бруска, если площадь внутренней части конструкции (квадрата ABCD) равна 144 кв. ед.

2.

Один из корней уравнения 2х² – mx – 3 = 0 равен x₀ = –0,5. Чему равно m?

3.

На гипотенузе АВ прямоугольного треугольника АВС отмечены точки D и E, причём ЕА = АС, а DB = ВС. Найдите ∠DCE.

4.

Новый год в доме Пущина встречали 30 человек, причем оказалось, что среди всех гостей 26 человек по имени Вова, а у остальных гостей имена оказались разные. В полночь все расселись за праздничным круглым столом, и каждый загадал одно желание. Как известно, исполняются желания только у тех, кто сидит между двумя людьми с одинаковыми именами. Какое наибольшее количество желаний может исполниться? А наименьшее?

5.

Можно ли разбить все натуральные числа от 1 до 9 на три группы по три числа так, чтобы в каждой группе самое большое число было равно сумме двух других чисел? Ответ объясните.

6.

На доске сначала было написано число 123456789. У написанного числа выбираются две соседние неравные нулю цифры, из каждой вычитается по 1, и выбранные цифры меняются местами. Эта операция повторяется несколько раз. Например, 123456789 → 123454789, а дальше 123454789 → 123454769. Какое наименьшее число может получиться в результате нескольких операций?

7.

На конференции собрались марсиане, у каждого из которых по 7 конечностей, и земляне, у каждого из которых по 4 конечности. У всех участников конференции вместе было 53 конечности. Определите наибольшее число землян, которые могли принимать участие в конференции.

8.

Четверо ребят — Алексей, Борис, Владимир и Григорий — участвовали в лыжных гонках. Все они пришли к финишу в разное время. На следующий день, на вопрос, кто какое место занял, они ответили следующим образом. Алексей: «Я не был ни первым, ни последним»; Борис: «Я не был последним»; Владимир: «Я был первым»; Григорий: «Я был последним». Известно, что три из этих ответов были правдивыми, а один — ложным. Так кто же все-таки был первым?

9.

В прямоугольнике со сторонами 4 и 10 биссектрисы всех углов проведены до взаимного пересечения. Найдите площадь четырехугольника, образованного биссектрисами.