МАЛЫЙ МЕХМАТ МГУ

Кружок 8 класса

Занятие 10. Математическая индукция

Пусть дана последовательность пронумерованных утверждений: Утв₁, Утв₂, Утв₃, ..., Утв_k, Утв_k+1, ... (конечная или бесконечная). Мы сможем доказать все эти утверждения, если докажем, что:
1) Утв₁ — истинно;
2) Если истинно Утв_k, то истинно и Утв_k+1 (для любого натурального номера k).
Действительно, в этом случае истинно первое утверждение (п.1), тогда по п.2 истинно и второе, а значит, и третье, и т.д.

Этот метод доказательства последовательности утверждений называется методом математической индукции. Он состоит из двух вышеуказанных этапов. Первый из них называется база индукции, а второй — переход индукции или шаг индукции.

1.

Докажите тождество: 1 + 3 + 5 + … + (2n − 1) = n² для любого натурального n.

Решение

Решение.

Эти тождества образуют последовательность утверждений, занумерованных числом n, а именно:
Утв₁: 1 = 1²
Утв₂: 1 + (2·2 − 1) = 1 + 3 = 2² = 4
Утв₃: 1 + 3 + 5 = 3²
...
Утв_k: 1 + 3 + 5 + … + (2k − 1) = k²
Утв_k+1: 1 + 3 + 5 + … + (2·(k + 1) − 1) = (k + 1)²
...
База индукции: докажем первое утверждение, то есть что 1 = 1². Но это очевидно.
Шаг индукции: докажем, что из Утв_k следует Утв_k+1. Пусть уже доказано, что 1 + 3 + 5 + … + (2k − 1) = k². Надо доказать, что тогда 1 + 3 + 5 + … + (2·(k + 1) − 1) = (k + 1)². Запишем: 1 + 3 + 5 + … + (2k − 1) + (2·(k + 1) − 1) = k² + (2k + 1) = (k + 1)². Здесь первое равенство выполняется, поскольку верно Утв_k.
Таким образом, доказаны база и шаг индукции, а значит, и требуемое Утв_n: 1 + 3 + 5 + … + (2n − 1) = n² доказано для любого натурального n.

2.

Известно, что x + ¹/_x — целое число. Докажите, что при любом целом n число xⁿ + ¹/_xⁿ — также целое.

Решение

Решение.

Сначала докажем это утверждение при n = 0. Но x⁰ + ¹/_x⁰ = 1 + 1 = 2 — целое, поэтому это утверждение очевидно. Если число n отрицательно, и n = -m, где m — натуральное, то xⁿ + ¹/_xⁿ = x ^{− m} + ¹/_{x ^{− m}} = x^m + ¹/_x^m. Поэтому достаточно доказать утверждение для натуральных n.

Применим метод математической индукции аналогично тому, как это сделано в предыдущей задаче.
База индукции: докажем, что если x + ¹/_x — целое, то x¹ + ¹/_x¹ — тоже. Но это очевидно, так как x¹ + ¹/_x¹ = x + ¹/_x.
Шаг индукции: Пусть известно (то есть доказано на предыдущих шагах индукции), что x + ¹/_x, x² + ¹/_x², x³ + ¹/_x³, …, x^{k − 1} + ¹/_{x^{k − 1}}, x^k + ¹/_x^k — целые числа. Докажем, что тогда x^{k + 1} + ¹/_{x^{k + 1}} — тоже целое. Для этого запишем: (x^k + ¹/_x^k)·(x + ¹/_x) = x^{k + 1} + ¹/_{x^{k − 1}} + x^{k − 1} + ¹/_{x^{k + 1}} = (x^{k + 1} + ¹/_{x^{k + 1}) + (x^{k − 1} + ^{/1}{x^{k − 1}}). Отсюда находим, что x^{k + 1} + ¹/_{x^{k + 1}} = (x^k + ¹/_x^k)·(x + ¹/_x) − (x^{k − 1} + ¹/_{x^{k − 1}}). Первое слагаемое в правой части этого равенства является произведением двух целых чисел по предположению, а значит, и само является целым. Второе слагаемое — тоже целое по предположению. Значит, их сумма — целое число. Тогда и в левой части равенства стоит целое число, что и требовалось доказать.

Упражнение. Как найти какое-нибудь число x, для которого x + ¹/_x = k, где k — заданное целое число? При каких целых k это можно сделать?

3.

Докажите неравенство 2ⁿ > n для произвольного натурального n.

Решение

Решение.
База индукции. Докажем, что 2¹ > 1. Но это очевидно.
Шаг индукции. Пусть известно, что 2^k > k. Докажем, что тогда 2^{k + 1} > k + 1. Запишем 2^{k + 1} = 2·2^k > 2· k > k + 1, если k > 1. Первое неравенство в этой цепочке вытекает из предположения о том, что 2^k > k.

4.

Найдите все натуральные n, при которых 2n не больше, чем n².

Ответ Решение

Ответ. n ≥ 2.

Решение.

Ясно, что при n = 1 утверждение неверно, так как 2·1>1². А вот при n = 2, n = 3, n = 4 оно уже верно (убедитесь в этом самостоятельно). Причем с увеличением числа n увеличивается и разность между числами n² и 2n. Это наводит на мысль, что 2n ≤ n² при всех натуральных n, бóльших единицы. Теперь строго докажем это по индукции.

База индукции: n = 2. Надо доказать, что 2·2 ≤ 2². Но это очевидно.
Шаг индукции. Пусть известно, что 2k ≤ k². Докажем, что 2(k + 1) ≤ (k + 1)². Запишем (k + 1)² = k² + 2k + 1 ≥ 2k + 2k + 1 = 2(k + 1) + 2k − 1 ≥ 2(k + 1), если 2k − 1 ≥ 0, в том числе при любом натуральном k, что и требовалось доказать.

Замечание. Эту задачу можно решить и без использования метода математической индукции. Пусть n ≥ 2. Домножим обе части этого неравенства на n (это можно сделать, так как если n ≥ 2, то n > 0). Получим n² ≥ 2n, что и требовалось доказать.

5.

В прямоугольнике размера 3×n стоят фишки трех цветов, по n штук каждого цвета. Докажите, что можно переставить фишки в каждой строке так, чтобы в любом столбце были фишки всех цветов.

Решение

Решение. Докажем это утверждение индукцией по n.
База индукции: n = 1. В прямоугольнике размера 3×1 находятся три фишки, каждая своего цвета. Тогда требование задачи уже выполнено, и вообще ничего переставлять не надо.
Шаг индукции. Пусть для любого прямоугольника размера 3×k (с указанным набором фишек) требуемая перестановка существует. Докажем, что она существует и для любого прямоугольника размера 3×(k + 1). Сначала переставим фишки так, чтобы в последнем, (k + 1)-м столбце все фишки были разноцветными. Ясно, что в оставшейся части прямоугольника (размера 3×k) находятся по k фишек каждого цвета. Применив наше предположение, расставим в этой части фишки требуемым образом. В результате в каждом из столбцов от первого до k-го фишки разноцветные по предположению, а в последнем столбце — по построению.

6.

Несколько прямых делят плоскость на части. Докажите, что эти части можно раскрасить в два цвета так, что любые две граничащие (то есть имеющие общую сторону) части будут раскрашены в разные цвета.

Решение

Решение. Докажем это утверждение индукцией по количеству прямых.
База индукции. Пусть на плоскости проведена всего одна прямая, которая делит эту плоскость на две части. Одну из этих частей покрасим в белый цвет, а другую — в черный. Тогда требование условия будет выполнено.
Шаг индукции. Пусть на плоскости проведено k прямых, и части плоскости раскрашены в черный и белый цвета требуемым образом. Проведем (k + 1)-ую прямую. Все части плоскости по одну сторону от этой новой прямой перекрасим в противоположные цвета, а по другую сторону оставим все без изменений (см. рисунок). Убедитесь, что в этом случае части плоскости будут раскрашены требуемым образом.

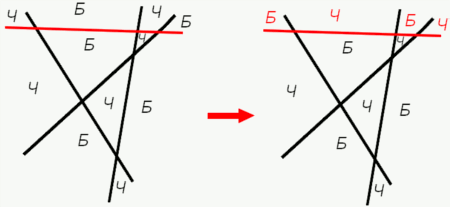
7.

Докажите, что 1· 1! + 2 · 2! + ... + n · n! = (n + 1)! − 1 для всех натуральных n (здесь n! = 1·2·3·...·n).

Решение

Решение. База индукции. Надо доказать, что 1·1! = (1 + 1)! − 1. Это верно, так как 1! = 1, 2! = 2.
Шаг индукции. Пусть доказано, что 1· 1! + 2 · 2! + ... + k · k! = (k + 1)! − 1. Докажем, что тогда 1· 1! + 2 · 2! + ... + k · k! + (k + 1)·(k + 1)! = (k + 2)! − 1. Запишем 1· 1! + 2 · 2! + ... + k · k! + (k + 1)·(k + 1)! = (k + 1)! − 1 + (k + 1)·(k + 1)! = (k + 1)!·(1 + k + 1) − 1 = (k + 1)!·(k + 2) − 1 = (k + 2)! − 1. Здесь мы пользовались тем, что (k + 1)!·(k + 2) = (k + 2)! (убедитесь, что это следует из определения числа (k!)).

8.

Для произвольного натурального n и вещественного x > -1 докажите неравенство Бернулли: (1 + x)ⁿ ≥ 1 + nx.

Решение

Решение. Докажем это утверждение индукцией по n.
База индукции: n = 1. Надо доказать, что (1 + x)¹ ≥ 1 + 1· x. Но это очевидно.
Шаг индукции. Пусть доказано, что (1 + x)^k ≥ 1 + kx. Докажем, что тогда (1 + x)^{k + 1} ≥ 1 + (k + 1)· x. Запишем (1 + x)^{k + 1} = (1 + x)^k·(1 + x) ≥ (1 + kx)·(1 + x) = 1 + kx + x + kx² ≥ 1 + (k + 1)· x, что и требовалось доказать. Здесь мы воспользовались тем, что при любом натуральном k и любом действительном x имеем kx² ≥ 0, а также предположением о том, что (1 + x)^k ≥ 1 + kx.

9.

Любую ли сумму из целого числа рублей, большего семи, можно уплатить без сдачи денежными купюрами по 3 и 5 рублей? Почему?

Ответ Решение

Ответ. Да, любую.

Решение. Ясно, что 8 = 3 + 5, 9 = 3 + 3 + 3, 10 = 5 + 5. Прибавляя к 8 нужное количество троек, можем получить любое число, делящееся на 3 с остатком 2. Прибавляя тройки к 9, получим все числа, делящиеся на 3 без остатка. А прибавляя тройки к 10, получим все числа, делящиеся на 3 с остатком 1. Проведите строгое доказательство самостоятельно. Для произвольного натурального n ≥ 8 укажите способ его представления в виде суммы троек и пятерок в зависимости от его остатка при делении на 3, основываясь на вышеизложенных соображениях.

10.

Коля Васин при помощи метода математической индукции смог доказать, что в любом табуне все лошади одной масти. Для этого он провел такие рассуждения: «Если есть только одна лошадь, то она своей масти, так что база индукции верна. Для перехода предположим, что есть n лошадей (с номерами от 1 до n). Пусть уже доказано, что в любом табуне из (n - 1) лошади все лошади одной масти. Значит, в нашем табуне все лошади с номерами от 1 до (n - 1) одинаковой масти. По тем же соображениям лошади с номерами от 2 до n одинаковой масти. Но лошади с номерами от 2 до (n - 1) не могут менять свою масть в зависимости от того, как они сгруппированы, — это ведь лошади, а не хамелеоны. Поэтому все n лошадей должны быть одинаковой масти». Есть ли ошибка в этом рассуждении, и если есть, то какая?

Ответ Решение

Ответ. Ну конечно же есть!

Решение. «Переход» индукции, предложенный Колей, не позволит нам доказать утверждение даже для табуна из двух лошадей. Первая лошадь своей масти, вторая — тоже. Однако никаких лошадей с промежуточными номерами нет. Поэтому и между нашими двумя лошадьми, вообще говоря, нет ничего общего.