МАЛЫЙ МЕХМАТ МГУ

Кружок 10 класса

Руководитель Дмитрий Александрович Коробицын
2009/2010 учебный год

Неравенства (13.02.2010)

1.
Даны три действительных числа с ненулевой суммой. Докажите, что сумма трёх попарных произведений их трёх попарных сумм больше суммы их трёх попарных произведений.
2.
Для действительных чисел a и b докажите неравенство
a2 + ab + b2 ≥ 3(a + b − 1).
3.
a, b, c — длины сторон некоторого треугольника. Докажите неравенство
a3 + b3 + 3abc > c3.
4.
Про положительные числа a, b, c, d известно, что abcd = 1. Докажите, что среди чисел (a2 + 1)/b2, (b2 + 1)/c2, (c2 + 1)/d2, (d2 + 1)/a2 есть число, не меньшее 2.
5.
a, b и c — положительные числа. Докажите неравенство:
a2 + b2 + c2 ≤ 2/3(a3 + b3 + c3) + 1.
6.
Произведение положительных чисел x, y и z равно 1. Докажите, что если
1/x + 1/y + 1/z ≥ x + y + z,
то для любого натурального k выполняется неравенство
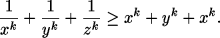
7.
Докажите, что если 0 < a, b < 1, то
ab(1 − a)(1 − b) < 1 .
(1 − ab)2 4
8.
Числа x1, x2, ..., xn принадлежат отрезку [a;b], где 0 < a < b. Докажите неравенство