МАЛЫЙ МЕХМАТ МГУ

Кружок 10 класса

Геометрия: площадь (30.01.2010)

1.

На продолжениях сторон DA, AB, BC, CD выпуклого четырёхугольника ABCD взяты точки A', B', C', D' так, что 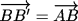, , 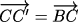, 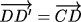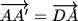. Докажите, что площадь четырёхугольника A'B'C'D' в 5 раз больше площади четырёхугольника ABCD.

2.

На окружности с центром O₁ радиуса r₁ взяты точки K и M. В центральный угол KO₁M вписана окружность с центром O₂ радиуса r₂. Найдите площадь четырёхугольника MO₁KO₂.

3.

а)

Каждая из диагоналей четырёхугольника делит его площадь пополам. Докажите, что этот четырёхугольник — параллелограмм.

б)

Каждая из диагоналей AD, BE и CF выпуклого шестиугольника ABCDEF делит его площадь пополам. Докажите, что эти диагонали пересекаются в одной точке.

4.

Точки K и M — середины сторон AB и CD выпуклого четырёхугольника ABCD, точки L и N расположены на двух других сторонах так, что KLMN — прямоугольник. Докажите, что S_ABCD = 2S_KLMN.

5.

Внутри треугольника ABC выбрана точка O. Докажите, что

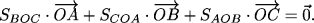
6.

A' — точка на одной из сторон трапеции ABCD такая, что прямая AA' делит её площадь пополам. Точки B', C', D' определяются аналогично. Докажите, что точки пересечения диагоналей четырёхугольников ABCD и A'B'C'D' симметричны относительно середины средней линии исходной трапеции.

7.

Треугольник ABC с острым углом A, равным α, вписан в окружность. Диаметр этой окружности проходит через основание высоты треугольника, проведённой из вершины B, и делит треугольник ABC на две части одинаковой площади. Найдите величину угла B.