МАЛЫЙ МЕХМАТ МГУ

Кружок 10 класса

Тригонометрия (21.11.2009)

1.

Докажите, что при всех положительных x и y и при всех действительных α справедливо неравенство x^{sin2 α} · y^{cos2 α} < x + y.

2.

Решите уравнение sin x + cos x = tg x + ctg x.

3.

Известно, что tg α + tg β = p, ctg α + ctg β = q. Найдите tg(α + β).

4.

Даны пять попарно различных чисел a₁, a₂, a₃, a₄, a₅. Докажите, что для некоторых i и j выполняется неравенство: .

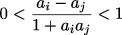5.

Найдите все углы α, при которых набор чисел sin α, sin 2α, sin 3α совпадает с набором cos α, cos 2α, cos 3α.

6.

Докажите, что при всех x таких, что 0 < x < ^π/₃ выполняется неравенство sin 2x + cos x > 1.

7.

Каждую вершину выпуклого четырёхугольника площади S отразили симметрично относительно диагонали, не содержащей эту вершину. Получили четырёхугольник площади S'. Докажите, что ^S'/_S < 3.

8.

Решите систему уравнений:

{	sin x	+	2 sin (x+y+z)	=	0
	sin y	+	3 sin (x+y+z)	=	0
	sin z	+	4 sin (x+y+z)	=	0