МАЛЫЙ МЕХМАТ МГУ

Кружок 10 класса

Задачи по стереометрии (24.10.2009)

1.

Площадь поверхности треугольной пирамиды равна S. Найдите площадь поверхности пирамиды, вершинами которой являются точки пересечения медиан граней данной пирамиды.

2.

Из отрезков с длинами 1, 1, 1, 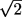, , 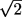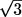составили тетраэдр. Какое наибольшее количество граней может оказаться прямоугольными треугольниками?

3.

В треугольной пирамиде ABCD рёбра AB и CD имеют длины a и b соответственно. Найдите сумму квадратов длин двух отрезков, один из которых соединяет середины AC и BD, а другой — середины BC и AD.

4.

Дан прямоугольный параллелепипед ABCDA₁B₁C₁D₁. Сравните расстояния от вершины A до плоскостей A₁BD и C₁BD.

5.

В пространстве дана замкнутая ломаная ABCDEF такая, что AB ∥ ED, BC ∥ EF, CD ∥ FA. При этом, AB ≠ ED. Верно ли, что все звенья ломаной лежат в одной плоскости?

6.

В пространстве расположены два единичных куба с общим центром. Докажите, что объем их пересечения больше ½.

7.

Проекции тела на две плоскости — круги. Докажите, что эти круги имеют одинаковые радиусы.

8.

В прямоугольном параллелепипеде одно из сечений является правильным шестиугольником. Докажите, что этот параллелепипед — куб.