МАЛЫЙ МЕХМАТ МГУ

Кружок 4 класса

Занятие 12 (12 декабря 2015 года). Геометрия

1.

Деревянный кубик с ребром 3 см покрасили снаружи в красный цвет и разрезали на кубики с ребром 1 см.
а) Сколько получилось кубиков?
б) Сколько кубиков имеют одну красную грань?
в) Сколько кубиков имеют две красные грани?
г) Сколько кубиков имеют три красные грани?
д) Сколько кубиков не имеют ни одной красной грани?

Ответ

Ответ. а) 27 кубиков; б) 6 – по одному на каждой грани в центре в) 12 – по одному на каждом ребре в центре г) 8 – каждая вершина д) 1 – центральный

2.

Для окраски квадратного пола со стороной 4 м требуется 4 кг краски. Сколько краски потребуется для окраски квадратного пола со стороной 8 м?

Ответ

Ответ. 16

3.

После семи стирок и длина, и ширина, и высота кубического куска мыла уменьшились вдвое. На сколько стирок хватит оставшегося куска?

Ответ

Ответ. На одну стирку.

4.

На глобусе провели 10 меридианов и 11 параллелей. Сколько кусков получилось? (Меридиан – это дуга от полюса до полюса, параллель – полный круг.)

Ответ

Ответ. 120

5.

Одну сторону прямоугольника уменьшили на 99 см, а другую увеличили на 1 см. Может ли площадь прямоугольника увеличиться?

Ответ

Ответ. Да, может. Например, 1 на 200. После изменений будет 2 на 101.

6.

Имеется три прямоугольных листа бумаги. Может ли так быть, что никакими двумя из них нельзя полностью накрыть третий?

Ответ

Ответ. Да, может. Например, 1 на 100, 4 на 4, 2 на 6.

7.

Квадрат 8 на 8 (площадь равна 64) разрезали на 4 части и из них сложили прямоугольник 5 на 13 (площадь равна 65). Получается, 64 равно 65? Найдите ошибку!

Объяснение

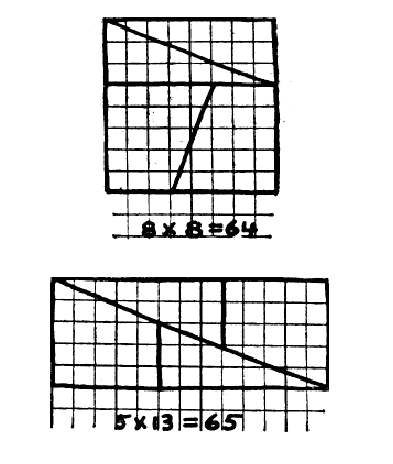Объяснение. На самом деле при складывании линии не прямые. Если аккуратно их проводить (или честно посчитать углы), будет видно, что они ломаные. Другими словами, там есть дырки. Если смотреть в обратную сторону (от прямоугольника к квадрату), получится, что в квадрате куски бы накладывались.

Дополнительные задачи

8.

От каждой вершины деревянного куба отпилили по одинаковому кусочку так, что место спила имеет форму треугольника. Сколько вершин и сколько ребер у получившегося тела?

Ответ

Ответ. Ответ: 24 вершины и 36 рёбер.

9.

Грань куба разделена на 4 равных квадрата, и каждый квадрат окрашен в один из трех цветов: красный, синий и зеленый так, что квадраты, имеющие общую сторону, окрашены в разные цвета. Сколько может быть красных квадратов? Решение перебором не принимается.

Решение Ответ

Решение. Посмотрим на вершину куба. Там соседствуют три стороны маленьких квадратов, значит, все три должны быть разных цветов. Получается, при каждой вершине всегда ровно один красный.

Ответ. 8