
МАЛЫЙ МЕХМАТ МГУ

Кружок 9 класса
Руководители Иван Александрович Дорофеев и Степан Львович Кузнецов
2005/2006 учебный год
2005/2006 учебный год
Листок 19. Задачи на максимум и минимум
- 1.
- На какие а) две части, б) n частей нужно разбить данное число, чтобы произведение их было наибольшим?
- 2.
- Найдите, при каких значениях x и y выражение xp yq имеет наибольшее значение, если x + y = a.
- 3.
- Докажите, что сумма а) двух, б) нескольких чисел, произведение которых неизменно, становится наименьшей, когда эти числа равны.
- 4.
- Когда произведение двух чисел, сумма которых неизменна, будет наибольшим?
- 5.
- Пусть x1 < x2 < ... < xn. Найдите такую точку x на числовой прямой, что сумма расстояний от x до xi принимает наименьшее значение.
- 6.
- а) Пусть a1 ≤ a2 и b1 ≤ b2. Докажите, что a1 b1 + a2 b2 ≥ a1 b2 + a2 b1. б*) Пусть a1 ≤ a2 ≤ ... ≤ an и b1 ≤ b2 ≤ ... ≤ bn. Докажите, что среди всех сумм попарных произведений ai bj, в которых каждое ai и каждое bj участвует ровно один раз, наибольшее значение имеет сумма a1 b1 + a2 b2 + ... + an bn.
- 7*.
-
(задача по геометрии) Найдите наименьшее значение выражения
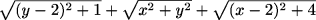 .
.
- 8.
- Докажите, что среди а) прямоугольников, б) ромбов с одинаковым периметром наибольшую площадь имеет квадрат. в) Какими должны быть стороны вписанного в окружность прямоугольника, чтобы его площадь была наибольшей?
- 9.
- Дана прямая l и две точки A и B, лежащие а) по разные стороны, б) по одну сторону от прямой l. Найдите такую точку X на прямой l, что AX + BX принимает наименьшее значение.
- 10.
-
Луч света, идущий из точки A, приходит в точку B, отразившись
от плоского зеркала (рис. 1). Докажите, что, подчиняясь закону отражения
(угол падения равен углу отражения), луч выбирает кратчайший путь.
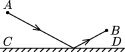
Рис. 1 - 11.
-
В стороне от прямолинейного участка железнодорожного пути, на расстоянии
d от него, лежит посёлок B (рис. 2). Где надо устроить полустанок C, чтобы проезд
от A по железной дороге AC и по шоссе CB отнимал как можно меньше
времени? Скорость движения по железной дороге равна v1, а по шоссе —
v2, v1 > v2.
![[рис.2]](p2.gif)
рис. 2 - 12*.
- (задача Ферма--Торричелли) Найдите точку, сумма расстояний от которой до вершин данного треугольника является наименьшей.
- 13*.
- (задача Фаньяно) Дан остроугольный треугольник ABC. Для каких точек K, L и M, лежащих на стронах BC, AC и AB соответственно, периметр треугольника KLM принимает наименьшее значение?
- 14*.
- (задача Дидоны) Докажите, что из всех фигур с заданной длиной границы наибольшей площадью обладает круг.