МАЛЫЙ МЕХМАТ МГУ

Кружок 6 класса

Руководитель Степан Львович Кузнецов
2014/2015 учебный год

Группа «А»

Группа «Б»

Группа «К» (ст. преп. Л. Н. Колотова)

Группа «В» (ст. преп. А. С. Воропаев)

Группа К (старший преподаватель Л. Н. Колотова)

Занятие 8 (15 ноября 2014 года). Геометрические конструкции

1.: Можно ли квадрат 4×4 без угловой клетки (см. рис. 1) разрезать на 3 равные части?

Рис. 1
2.: Можно ли уголок из трех клеток (см. рис. 2) разрезать на 4 равные части?

Рис. 2
3.: Разрежьте фигуру, изображенную на рисунке 3, на 4 равные части.

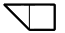
Рис. 3
4.: Разрежьте прямоугольник 3×8 на 6 одинаковых прямоугольников. На 7 одинаковых прямоугольников?
5.: Можно ли разрезать квадрат на 2000 равных треугольников?
6.: Разрежьте уголок (см. рис. 2) на 4 части, из которых можно сложить треугольник. А на три части? А на две?
7.: Как посадить 9 деревьев так, чтобы получилось 10 прямых рядов по три дерева в каждом?
8.: Приведите пример карты, на которой четыре треугольные страны граничат каждая с каждой.
9.: На рисунке 4 изображена часть крепостной стены. Один из камней имеет столь причудливую форму, что если его вытащить из стены и положить иначе, то стена станет ровной. Изобразите этот камень!

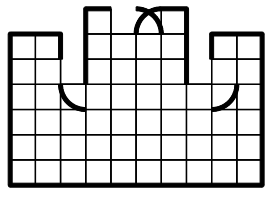
Рис. 4
10.: Сколько существует различных фигурок пентамино (из пяти клеточек)? Выложите все пентаминошки (каждого вида по одной) в прямоугольник 6×10.