МАЛЫЙ МЕХМАТ МГУ

Кружок 6 класса

Занятие 7 (8 ноября 2014 года). Раскраски

1.

Какую клетку можно выпилить в доске 5×5, чтобы оставшуюся часть можно было разрезать на доминошки? (Каждая доминошка покрывает ровно две клетки доски.)

2.

У шахматной доски выпилены две противоположные угловые клетки. Можно ли такую испорченную доску распилить на доминошки?

3.

Конь вышел с некоторого поля шахматной доски и через некоторое число ходов вернулся на это же поле. Докажите, что он сделал четное число ходов.

4.

Можно ли хромым королем (король не может ходить по диагонали) обойти по одному разу все клетки шахматной доски, начав в левом нижнем углу и закончив в правом верхнем углу?

5.

Можно ли разрезать прямоугольник 4×5 на 5 различных фигурок «тетрамино» (фигурки, составленные из четырех клеток, как-то примыкающих друг к другу по стороне)?

6.

В каждой клетке на доске 7×7 сидит по миньону.

7. а)

По команде все миньоны переползают на одну из соседних по стороне клеток. Докажите, что после этого по крайней мере 1 клетка окажется свободной.

8. б)

По команде все миньоны переползают на одну из соседних по диагонали клеток. Докажите, что после этого по крайней мере 7 клеток окажется свободными.

9.

На доске 8×8 для "морского боя" стоит 3-палубный корабль. Какое наименьшее число выстрелов необходимо сделать, чтобы наверняка ранить его?

10.

На шахматной доске стоит несколько королей. Докажите, что их можно раскрасить в четыре цвета так, чтобы короли одного цвета не били друг друга.

11.

В фирме 1111 сотрудников. Каждый из них обязан отработать в году 7 дней подряд на уборке территории. Докажите, что найдется 7 дней в году (не обязательно идущих подряд), что на уборке в этот день работало нечетное число сотрудников.

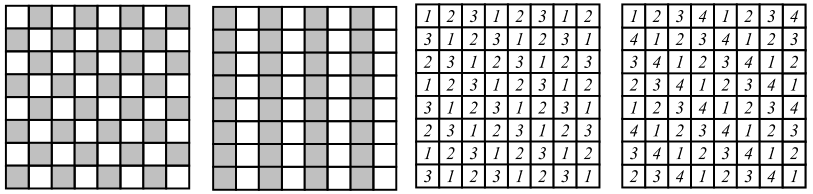
При решении задач этого листика вам помогут шахматная раскраска, раскраска в полоску, раскраска по диагоналям (в 3,4 цвета).