|
Избранные задачи домашних олимпиад
Часть III
|
321.
| У Тани и Димы денег поровну. Какую часть своих денег должна Таня отдать Диме, чтобы у неё стало в два раза меньше денег, чем у него?
| |
322.
| Несколько учащихся ушли из лицея и несколько пришли. В результате число учащихся уменьшилось на 10%, а доля мальчиков в лицее увеличилась с 50% до 55%. Увеличилось или уменьшилось число мальчиков? | Ответ
Указание | |
|
Указание. 0,9 · 0,55 = 0,495 < 0,5. | | |
| |
323.
| Сумма двух натуральных чисел равна 474. Одно из них оканчивается цифрой 1. Если эту цифру зачеркнуть, то получится второе число. Найдите эти числа.
| |
324.
| а) Закрасьте несколько клеток квадрата 4×4 так, чтобы любая закрашенная клетка имела общую сторону ровно с тремя незакрашенными, а любая незакрашенная — ровно с одной закрашенной. | Ответ |
Ответ.
| | |
б) Раскрасьте клетки квадрата 4×4 так, чтобы для любой клетки ровно одна соседняя с ней по стороне клетка была противоположного цвета. | Ответ |
Ответ.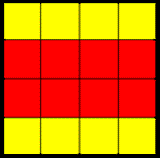 
| | |
| |
325.
| В полдень самолёт вылетел из столицы в город Энск и приземлился там в 14 часов местного времени. В полночь по местному времени он вылетел обратно и оказался в столице в 6 часов утра. Сколько времени длился полёт от столицы до Энска? | Ответ
Решение
| |
Решение. С полудня до 6 часов утра следующих суток прошло 12 + 6 = 18 часов. Самолёт стоял на земле 24 – 14 = 10 часов. Следовательно, полёт от столицы до Энска длился (18 – 10) : 2 = 4 часа. | |
|
| |
326.
|  Найдите величину угла между минутной и часовой стрелками часов в а) 9 часов 20 минут; б) 10 часов 10 минут.
| Ответ пункта а)
Ответ пункта б)
Указание к пункту б)
| |
| |
Указание. б) Вообразим, что часовая стрелка застыла на цифре 9, а минутная движется от 12 вплоть до 4. Не следует говорить, конечно, что угол составил бы 210°, поскольку этот угол больше развёрнутого. Лучше рассмотрим дополнительный угол величиной 360 – 210 = 150°.
Теперь вспомним, что часовая стрелка на месте не стояла. Поскольку часовая стрелка движется в 12 раз медленнее минутной, а минутная повернулась на 120°, то часовая стрелка за 20 минут поворачивается на 10°. Следовательно, величина угла между часовой и минутной стрелками в 10 часов 10 минут равна 150 + 10 = 160°. | |
|
| |
327.
| За 11 тугриков дают 14 динаров, за 22 рупии — 21 динар, за 5 крон — 2 талера, а за 10 рупий — 3 талера. Сколько тугриков можно выручить за 13 крон?
| Ответ
Указание | |
|
Указание. Отношение стоимости тугрика к стоимости динара равно 14 : 11, динара к рупии 22 : 21, рупии к талеру 3 : 10, а талера к кроне — 5 : 2. Перемножьте эти дроби. | |
|
| |
328.
|  Покрасьте клетки доски 5×5 в пять цветов так, чтобы в каждом горизонтальном ряду, в каждом вертикальном ряду и в каждом выделенном блоке все цвета встречались по одному разу.
| Указание I
Указание II
Указание III
Указание IV
Указание V
Ответ |
|
Указание I.
 Закрасим сразу целый блок зелёной, жёлтой, красной, синей и оливковой красками.
Мы при этом ничем не рискуем: любая другая соответствующая условию задачи раскраска этого блока отличается от нашей лишь выбором цветов. | |
| Указание II. Как обычно, пронумеруем строки числами от 1 до 5 (снизу вверх, то есть нижняя строка — первая), а столбцы — слева направо буквами латинского алфавита: a, b, c, d.
Поскольку клетка a3 находится на одной вертикали с оливковой, синей, жёлтой и зелёной клетками, то она не может быть окрашена ни в один из этих цветов и поэтому должна быть красной. | |
|
Указание III.
 В «верхнем» блоке (точнее говоря, в блоке, образованном клетками b5, c5, d5, c4 и d4) должна быть красная клетка, причём эта клетка не может располагаться на четвёртой горизонтали (в самом деле, четвёртая горизонталь уже занята красной клеткой b4). Поэтому красной клетке «правого верхнего» блока (состоящего из клеток d2, d3, e3, e4 и e5) некуда деться, кроме как на d2.
 Следовательно, красная клетка «верхнего» блока — это обязательно c5. А для последней, пятой клетки доски осталось единственное поле — e1.
| | |
Указание IV.
 Теперь займёмся синим цветом. В «верхнем» блоке есть две возможности: b5 и d5. Но, закрасив синим цветом клетку b5, мы не сможем покрасить в синий цвет ни одну из клеток «левого нижнего» блока. Поэтому синяя клетка — не b5, а d5. | |
|
Указание V. Теперь легко определить цвет клетки b5: зелёный, поскольку на одной вертикали с ней находятся жёлтая и красная, а на одной горизонтали — оливковая и синяя (на одной горизонтали с клеткой b5 расположена и красная клетка c5, но об этом можно и не упоминать). Рассматривая верхнюю горизонталь, видим: клетка e5 должна быть жёлтой. После этого нетрудно понять, что клетка d3 оливкового цвета, e3 — синяя. Действуя таким образом, мы потихонечку «расшифруем» всю раскраску. | |
| Ответ. 
| |
|
| |
329.
| Какое четырёхзначное число в 83 раза больше своей суммы цифр?
| Ответ
Указание
| |
| Указание. Воспользовавшись тем, что любое натуральное число при делении на 9 даёт такой же остаток, что и сумма его цифр, докажите, что искомое число делится на 9. (А следовательно, и на 9 · 83 = 747.) | |
|
| |
330.
| Числа 2, 4, 8, 16, 32, 64, 128, 256 и 512 расставьте в клетках таблицы 3×3 так, чтобы произведения по всем вертикалям, горизонталям и обеим главным диагоналям были равны. | Указание I
Указание II
Ответ |
|
Указание I. Представьте эти числа в виде степеней двойки: 2 = 21, 4 = 22, 8 = 23, 16 = 24, 32 = 25, 64 = 26,
128 = 27, 256 = 28, 512 = 29; затем составьте из чисел 1, 2, ..., 8, 9 таблицу размером 3×3 таким образом, чтобы суммы по всем вертикалям, горизонталям и обеим главным диагоналям были равны.
| |
|
Указание II. Поскольку 1 + 2 + 3 + ... + 8 + 9 = 45,
а 45 : 3 = 15, то суммы должны равняться числу 15.
| |
|
|
Ответ. В следующей таблице суммы по всем вертикалям, горизонталям и обеим главным диагоналям одинаковы: Осталось возвести двойку в соответствующие степени — и задача решена:
| |
|
| |
331.
| В одной куче 18 конфет, в другой — 23. Двое по очереди съедают одну из куч, а другую делят на две кучи. Кто не может поделить (если в куче одна конфета), проигрывает. Есть ли у начинающего выигрышная стратегия?
|
Ответ
Решение |
|
|
Решение. Начинающий может съесть 23 конфеты и оставить сопернику две кучи, в каждой из которых нечётное число конфет (например, по 9 конфет в каждой куче). Второй игрок вынужден будет одну из куч съесть, а другую он разобьёт на две кучи, в одной из которых чётное число конфет, а в другой — нечётное. Первый игрок опять съест ту кучу, в которой нечётное число конфет, а кучу, в которой конфет чётное число, разобьёт на две кучи, в каждой из которых нечётное число конфет. Так они и будут играть до тех пор, пока второй не проиграет. | | |
| |
332.
| Поля клетчатой доски размером 8×8 будем по очереди закрашивать так, чтобы после окраски каждой очередной клетки фигура, состоящая из закрашенных клеток, имела ось симметрии. Покажите, как можно закрасить 28 клеток, соблюдая это условие. (В качестве ответа расставьте на тех клетках, которые должны быть закрашены, числа от 1 до 28 в том порядке, в котором проводилось закрашивание.) | Ответ
Пояснение
|
|
Ответ.
| |
| |
| |
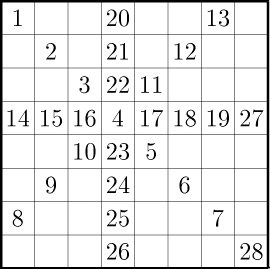
333.
| Мышка грызёт куб сыра с ребром 3, разбитый на 27 единичных кубиков. Когда мышка съедает какой-либо кубик, она переходит к кубику, имеющему общую грань с предыдущим. Может ли мышка съесть весь куб кроме центрального кубика (именно там, в центральном кубике, спрятан крючок мышеловки)? А если бы куб имел размеры 333×333×333?
|
Ответ
Комментарий |
Ответ. Раскрасим кубики в белый и чёрный цвета в шахматном порядке, а именно, пусть белыми будут 12 кубиков, расположенных в серединах рёбер большого куба (то есть кубики, ровно две грани каждого из которых расположены на поверхности большого куба), а остальные 14 кубиков пусть будут чёрными. Мышка не сможет съесть указанные 26 кубиков, поскольку в противном случае их можно было бы разбить на 13 пар, каждая из которых состояла бы из белого и чёрного кубика, а тогда белых и чёрных кубиков было бы поровну. | | |
Комментарий. Эта задача заимствована из «Зарубежных математических олимпиад» С.В. Конягина, Г.А. Тонояна, И.Ф. Шарыгина, И.А. Копылова, М.Б. Севрюка,
М.Л. Ситникова, О.А. Байбородина, В.П. Буриченко, Г.В. Головина, Д.О. Орлова, Л.Б. Парновского, Т.А. Соковой, И.В. Стеценко, В.В. Титенко и С.А. Филиппова. Номер задачи — 26.3. |
|
|
|
|
