|
Индукция
...выпросился остаться одну ночку; от одной
ночки две ночки, от двух ночек две недели,
от двух месяцев два года, а от двух годов
жил тридцать лет.
|
225.
| Придумайте 10 различных натуральных чисел,
сумма которых делится на каждое из них.
|
Указание
|
|
Указание.Сначала придумайте три числа, сумма которых делится на каждое из них. Потом подумайте, нельзя ли получить четыре таких числа,...
| |
|
|
|
226.
| Делится ли число 11...11 (восемьдесят одна
единица) на 81?
|
Решение
|
|
Решение.
111 делится на 3, 111 111 111 делится на 9,
111 111 111 111 111 111 111 111 111 =
111 111 111 · 1 000 000 001 000 000 001
делится на 9 · 3 = 27. Далее, представляя записанное
81 единицей число в виде произведения числа, записанного 27
единицами, и числа, три цифры которого — единицы, а остальные —
нули, ответьте на вопрос задачи.
Второй способ.
111 111 111 : 9 = 12345679. Значит, частное от деления числа
11...11 (81 единица) на 9 равно
12 345 679 012 345 679 012 345 679 012 345 679 012 345 679 012 345 679 012 345 679 012 345 679 012 345 679.
Осталось вспомнить признак делимости на 9.
| |
|
|
|
227.
| Разрежьте квадрат на а) 6; б) 7 квадратов.
в) Укажите все значения n, для которых квадрат нельзя разрезать на n меньших квадратов.
|
а) Ответ
б) Ответ
в) Ответ
| |
|
б) Ответ. Квадрат легко разрезать на 4 квадрата:
Разрезав один из четырёх равных квадратов на 4 равных квадрата, получаем искомое разрезание:
| |
|
в) Ответ. 2, 3 и 5. А именно, для всякого чётного n = 2k > 2 квадрат размером k×k можно разрезать на квадрат размером (k – 1)×(k – 1) и 2k – 1 единичных квадратов, а для всякого нечётного
n = 2k + 1 > 5 можно сначала некоторый квадрат разрезать на n – 3 = 2k – 2 квадратов, а затем один из квадратов разрезать на 4 равных квадрата.
| | |
г) При каких n равносторонний треугольник нельзя разрезать на n меньших равносторонних треугольников?
|
|
228.
| 
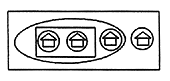В посёлке 100 домов. Сколько
заборов, не пересекающих друг друга, можно построить, чтобы
каждый забор огораживал хотя бы один дом и никакие два забора не
огораживали одну и ту же совокупность
домов?
|
Указание
Решение
|
|
Указание.
Решите задачу сначала не для 100, а для меньших
чисел: 1, 2, 3,... .
|
|
|
|
Решение.
Ответ для n домов: можно построить
2n - 1 заборов. В самом деле,
если дом один, то можно построить
только один забор, что соответствует формуле
2 · 1 - 1 = 1.
Дальше применим индукцию. Если для 1, 2,...,
(n - 1) домов
формула 2n - 1 уже проверена, то рассмотрим
n домов, вокруг
которых построено максимально возможное количество заборов.
Какой-то один забор огораживает все дома. Если этот внешний
забор снести, то самыми внешними станут некоторые два забора.
Внутри одного из них будет некоторое число k домов, а внутри
другого — остальные n - k
домов. Поскольку k < n, вокруг
k домов может быть построено, самое большее,
2k - 1 заборов.
Аналогично, вокруг остальных n - k домов может быть постороено,
самое большее, 2(n - k) - 1 заборов.
Значит, всего заборов не более
(2k - 1) + (2(n - k) - 1) + 1 = 2n - 1.
|
|
|
|
|
