
|
Избранные задачи домашних олимпиад
Часть II
|
308.
| На какое наименьшее число частей надо разрезать торт, чтобы его можно было раздать поровну как троим, так и четверым?
| Предупреждение
Указание
Ответ |
Предупреждение. Части не обязательно одинаковые. Ответ 12 (=НОК[3,4]) неверен. | |
| Указание. Если торт разрезан на 5 частей и эти части розданы поровну троим, то хотя бы одному из троих досталась всего лишь одна часть. В таком случае эта часть составляет 1/3 торта. Поскольку 1/3 > 1/4, то в рассматриваемом случае торт нельзя поровну раздать четверым. | |
|
Ответ. На 6 частей, а именно, три четверти и ещё три части по 1/12 каждая:

| |
|
| |
309.
| В скачках участвуют три лошади. Игрок может поставить некоторые (не обязательно одинаковые) суммы денег на каждую из них. Ставку на первую лошадь принимают в отношении 1 : 4. Это означает, что если первой прибежит первая лошадь, то игрок теряет деньги, поставленные на вторую и третью, но ему возвращают деньги, поставленные на первую, и ещё четыре раза по столько же. На вторую лошадь ставки принимают в отношении 1 : 3, а на
третью — 1 : 1. Можно ли поставить деньги так, чтобы выиграть при любом исходе скачек? (Разумеется, считайте, что хотя бы одна лошадь прибегает первой: ситуация, когда ни одна из лошадей не достигает финиша, очевидно проигрышная для игрока и поэтому её не надо рассматривать.) |
Ответ
Решение |
|
Решение. Если поставить на первую лошадь 20 копеек, на вторую — 25, а на третью — 50 копеек, то в любом случае игрок получит
1 рубль, а потратит лишь 20 + 25 + 50 = 95 копеек. | |
| |
310.
| Какое наибольшее число сторон может иметь многоугольник, являющийся пересечением четырёхугольника и треугольника?
| Ответ
Указание I
Указание II
Решение | |
Указание I. Четырёхугольник может быть невыпуклым. | |
|
Указание II. На рисунке изображено неверное решение: пересечение изображённых фигур — треугольника и четырёхугольника — состоит из двух четырёхугольников, а мы хотим, чтобы оно было восьмиугольником.
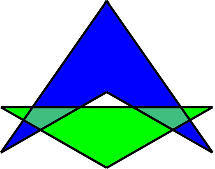
| |
|
|
Решение. 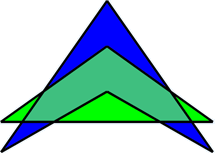
| |
|
| |
311.
| а) Конь вышел с некоторого поля шахматной доски и через несколько ходов вернулся на него. Докажите, что он сделал чётное число ходов. | Указание |
Указание. Каждым ходом конь меняет цвет поля: с белого поля идёт на чёрное, а с чёрного — на белое. | | |
б) Из шахматной доски выпилено угловое поле. Может ли конь обойти все оставшиеся поля по одному разу и вернуться на исходное поле?
| Ответ
Указание | |
|
Указание. Белых и чёрных полей на доске, из которой выпилили одно поле, не поровну. | | |
в) Может ли конь пройти из левого нижнего угла шахматной доски в правый верхний, побывав на каждом поле ровно один раз?
| Ответ
Указание | |
|
Указание. Поскольку число 63 нечётно, конь за 63 хода меняет цвет поля. Но левое нижнее и верхнее правое поля шахматной доски одного цвета (чёрные, хотя это не имеет значения). | | |
| |
312.
| 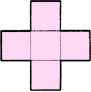 Крест составлен из пяти равных квадратов. Разрежьте его на такие части, из которых можно (без дыр и перекрытий) составить квадрат. Крест составлен из пяти равных квадратов. Разрежьте его на такие части, из которых можно (без дыр и перекрытий) составить квадрат.
| Указание |
Указание. 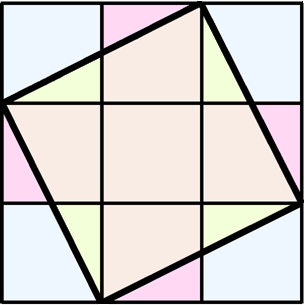
| | | |
| |
313.
| Если от некоторого двузначного числа отнять 2, то результат разделится нацело на 3, а если отнять не 2, а 3, то разделится не на 3, а на 2. Если к этому числу прибавить 4, то результат разделится нацело на 5, а если от него отнять 5, то разделится на 4. Более того, если от этого числа отнять 5, то разделится нацело на 6, а если же от нашего числа отнять 6, то разделится на 5. И это ещё не всё: если к этому замечательному числу прибавить 7, то результат разделится на 8, а если прибавить 8, то разделится на 7. Что же это за число?
| |
314.
| Придумайте 10 натуральных чисел, у которых и сумма, и произведение равны 20. | Намёк
Указание
Ответ
|
Намёк. Многие из искомых чисел равны 1. | | |
|
Указание. Найдите хотя бы одно решение уравнения 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + x + y = 1 · 1 · ... · 1 · x · y
в натуральных числах.
| |
|
Ответ. 1, 1, 1, 1, 1, 1, 1, 1, 2 и 10. | | |
| |
315.
|
а) Когда комиссия приехала в больницу, там находились 3 врача и 1996 пациентов. Комиссия попросила каждого указать двух врачей. Каждый врач назвал двух других врачей, а пациенты называли кого угодно. Докажите, что комиссия смогла выявить хотя бы одного пациента. |
Подсказка
Решение |
|
Подсказка. Врачи указали друг на друга. Могли ли все пациенты разбиться на тройки, в каждой из которых все указали друг на друга? | |
| Решение. Если человек не входит в тройку, в которой все указали друг на друга, то он не может быть врачом. Число 1999 не кратно трём. | |
|
б) В Конторе работают 200 психически здоровых и 1999 сумасшедших сотрудников. Однажды каждый сотрудник написал докладную записку, в которой перечислил 1999 своих коллег, по его мнению, сумасшедших. Каждый психически здоровый сотрудник верно указал всех сумасшедших, а каждый сумасшедший мог указать на кого угодно, кроме себя. Докажите, что на основании этих данных можно выявить по крайней мере 199 сумасшедших.| Указание
Решение |
|
Указание. Рассортируйте докладные записки на пачки, где указаны одни и те же сотрудники. Письма психически здоровых чекистов окажутся в отдельной пачке. | |
|
|
Решение. Рассортируем записки на пачки, собрав вместе те, где указаны одни и те же сотрудники. Выберем пачки, в которых количество записок не кратно числу 200. Поскольку записки здоровых сотрудников оказались в отдельной пачке, а количество всех записок даёт остаток 199 при делении на 200, то в выбранных пачках содержится не менее 199 записок. | |
|
| |
316.
| По кольцевой линии метро курсируют 24 поезда. Они идут в одном направлении с одинаковыми скоростями и равными интервалами. Сколько поездов надо добавить, чтобы при той же скорости уменьшить интервалы на 1/5?
| |
317.
| В одной из трёх комнат сидит принцесса, в другой — тигр, а в третьей нет никого. На двери левой комнаты написано: «Тигр в правой комнате», на двери средней: «Левая комната пуста», на двери правой: «Принцесса в средней комнате». Известно, что надпись на двери комнаты, где сидит принцесса, истинна, надпись на двери комнаты, где сидит тигр — ложна, а надпись на двери пустой комнаты может быть как истинной, так и ложной. Где сидит принцесса, а где — тигр?
| Ответ |
Ответ. Принцесса в левой комнате, а тигр в правой. | | |
| |
318.
| 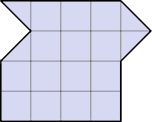 Разрежьте изображённую на рисунке фигуру на а) четыре; б) пять одинаковых частей. (Резать можно не только по сторонам и диагоналям клеток.) Разрежьте изображённую на рисунке фигуру на а) четыре; б) пять одинаковых частей. (Резать можно не только по сторонам и диагоналям клеток.)
|
а) Первый способ
Второй способ
б) Ответ
|
а) Первый способ. 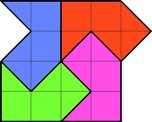
| |
|
а) Второй способ. 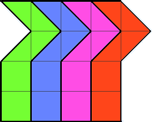
| |
|
|
б) Ответ.

| |
|
|
|
319.
| Представьте число 203 в виде суммы нескольких натуральных чисел, произведение которых тоже равно 203.
| Указание
Ответ |
Указание. Разложите число 203 на множители. | |
|
Ответ. 203 = 7 · 29 · 1 · ... · 1 (всего 203 – 7 – 29 = 167 единиц). | |
|
| |
320.
| Какое наибольшее количество чисел можно выбрать из набора 1, 2,..., 1963, чтобы сумма любых двух выбранных чисел делилась на 26? |
Ответ
Указание
| |
|
|
Указание. Рассмотрите числа, дающие остаток 13 при делении на 26. Поскольку 1963 = 75 · 26 + 13, то таких чисел существует 76 штук. | | |
|
|





 Крест составлен из пяти равных квадратов. Разрежьте его на такие части, из которых можно (без дыр и перекрытий) составить квадрат.
Крест составлен из пяти равных квадратов. Разрежьте его на такие части, из которых можно (без дыр и перекрытий) составить квадрат.
 Разрежьте изображённую на рисунке фигуру на
Разрежьте изображённую на рисунке фигуру на 

