
МАЛЫЙ МЕХМАТ МГУ

Кружок 7 класса
Руководитель Степан Львович Кузнецов
2011/2012 учебный год
2011/2012 учебный год
Занятие 23 (7 апреля 2012 года). Графы III
- 1.
- Группа островов соединена мостами так, что от каждого острова можно добраться до любого другого. Турист обошёл все острова, пройдя по каждому мосту ровно один раз. На острове A турист побывал трижды. Сколько мостов ведёт с острова A, если турист а) не с него начал и не на нём закончил; б) с него начал, но не на нём закончил; в) с него начал и на нём закончил?
- 2.
-
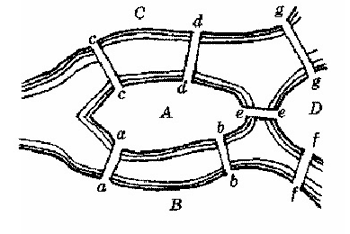
Задача Эйлера о кёнигсбергских мостах. Город Кёнигсберг (ныне Калининград) был расположен на берегах реки Прегель (ныне Преголя)
и двух островах, которые соединены семью мостами, как показано на рисунке. Можно ли было прогуляться по городу, пройдя по каждому мосту ровно один раз?
- 3.
-
- а)
- Квадрат со стороной n (n ≥ 3) разбит перегородками на единичные квадратики. Какое минимальное число перегородок нужно убрать, чтобы из каждого квадратика можно было добраться до границы квадрата?
- б)
- Куб со стороной n (n ≥ 3) разбит перегородками на единичные кубики. Какое минимальное число перегородок между единичными кубиками нужно удалить, чтобы из каждого кубика можно было добраться до границы куба?
- 4.
- Можно ли раскрасить рёбра куба в чёрный и белый цвета так, чтобы из любой вершины можно было перейти в любую другую, двигаясь только по чёрным рёбрам, а также двигаясь только по белым рёбрам?
* * *
- 5.
- На столе лежит кучка из 100 камней и чистый листок бумаги. Кучку разделяют на две произвольным образом, а на листке записывают произведение количеств камней в получившихся частях. Потом эту же процедуру повторяют каждой из образующихся кучек до тех пор, пока не останутся 100 «кучек» из одного камня. Чему может быть равна сумма всех записанных на листке чисел? (Укажите все возможные ответы.)
- 6.
- В тетради нарисованы несколько окружностей, которые можно обвести ручкой, не отрывая её от бумаги. Покажите, как это сделать, не проводя одну линию более одного раза.
- 7.
- Докажите, что вершины произвольного графа (без петель и кратных рёбер) можно раскрасить в два цвета так, чтобы не менее половины его рёбер оказались разноцветными.
* * *
- 8.
- Докажите, что вершины произвольного графа без петель и кратных рёбер можно раскрасить в три цвета так, чтобы не менее двух третей его рёбер оказались разноцветными.
- 9.
- Можно ли раскрасить вершины произвольного графа без петель и кратных рёбер в два цвета так, чтобы не менее а) 3/4; б) 501/1000 его рёбер оказались разноцветными?