
МАЛЫЙ МЕХМАТ МГУ

Кружок 8 класса
Руководитель Елена Сергеевна Суханова
2008/2009 учебный год
2008/2009 учебный год
Задание 8 - Индукция
О методе Математической Индукции
Основная схема.Метод индукции требует установления истинности двух фактов:
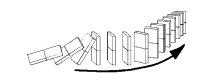
База: Первое утверждение верно. (мы можем толкнуть первую доминошку)
Переход: Если интересующее нас утверждение верно на каком-то шаге, то верно и следующее за ним утверждение. (толкнув одну, уроним и другую)
Часть 1. Вспомни
- 1.
-
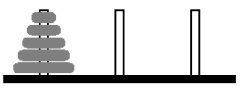
Ханойские башни. Есть три стержня и несколько колец разного размера. Класть можно только кольцо меньшего размера на кольцо большего размера. Можно ли переместить пирамидку с одного стрежня на другой, если в пирамидке:
- a)
- 2 кольца;
- b)
- 3 кольца;
- c)
- 5 колец;
- d)
- n колец.
- 2.
-
Рассмотрим уголок.
Он получается вырезанием из квадрата 2*2 одной клетки. Можно ли разрезать на такие уголки квадрат следующих размеров без одной клетки (вырезана может быть любая клетка квадрата, даже откуда-то из середины)?

- a)
- 4*4
- b)
- 8*8
- c)
- 128*128
- d)
- 2n*2n
- 3.
- Плоскость разбита на области n прямыми. Докажите, что вне зависимости от расположения прямых, можно так раскрасить эти области в черный и белый цвета, что никакие две области одного цвета не будут иметь общего участка (отрезка) границы.
Часть 2. Придумай
- 4.
-
У бородатого многоугольника во внешнюю сторону растет щетина. Его пересекает несколько прямых, на каждой из которых с одной из сторон тоже растет щетина. В результате многоугольник оказался разбитым на некоторое число частей. Докажите, что хотя бы одна из частей окажется бородатой снаружи.
- 5.
-
Докажите, что для любого натурального n справедливы неравенства
- a)
- 2n > n
- b)
- 1 + 2 + … + n ≤ n²
- 6.
- Докажите, что для произвольного натурального n верно равенство: 1 + 3 + … + (2n − 1) = n²
- 7.
- В пробирке живут амёбы. Каждую минуту происходит следующее: каждая амёба делится пополам, после чего в пробирку добавляют еще одну такую же амёбу. В начальный момент времени там была всего одна амёба. Докажите, что через n минут в пробирке будет 2n + 1 − 1 амёба.
- 8.
- Ханойские башни. За какое минимальное число перекладываний можно переместить пирамидку с одного стержня на другой.
- 9.
- На плоскости нарисовано несколько попарно пересекающихся окружностей (каждая окружность пересекается с любой другой). Доказать, что эту картинку можно обвести "одним росчерком", то есть не проходя по одной дуге два раза и не отрывая карандаша от бумаги, и при этом вернуться в начальную точку.
- 10.
- 10.Доказать, что для любого натурального n сумма углов в выпуклом (n + 2)-угольнике равна n * 180.