МАЛЫЙ МЕХМАТ МГУ

Кружок 5 класса

Круги Эйлера (9 марта 2013 года)

Понять, что такое круги Эйлера, можно, решив несколько задач. Каждый круг Эйлера обозначает множество объектов (то есть набор каких-либо объектов, заданный так, что про вообще любой объект можно однозначно определить, есть он в этом наборе, или нет), а точка — один объект. Точка рисуется внутри круга, если объект принадлежит этому множеству, а иначе — снаружи круга.

В случае, если объект принадлежит сразу нескольким множествам (то есть лежит в пересечении множеств), обозначающая его точка находится в пересечении соответствующих этим множествам кругов (то есть в каждом из них).

Если объект принадлежит хотя бы одному из нескольких множеств, то говорят, что он принадлежит их объединению. Применительно к кругам Эйлера это означает, что точка лежит хотя бы в одном из кругов, соответствующих этим множествам.

Объект лежит в разности двух множеств, если он лежит в первом из них, но не лежит во втором.

Чтобы не рисовать точки, часто просто пишут их количество в соответствующих частях кругов.

1.

На доске нарисованы два круга, внутри которых отмечено несколько точек. Внутри первго из них всего 190 отмеченных точек. Внутри второго — всего 230 отмеченные точки. Внутри обоих кругов одновременно находится ровно 70 точек. А сколько отмеченных точек всего?

Решение

Решение.

Сложим количества точек в обоих кругах. При этом точки, находящиеся в их пересечении (то есть и в первом, и во втором), будут посчитаны дважды, то есть лишний раз, поэтому от суммы нужно отнять число точек в пересечении. Теперь получим тот же ответ с помощью математических обозначений.

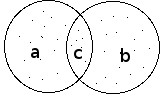
Введём обозначения:
a — количество точек, лежащих только в первом круге;
b — только во втором круге;
c — в их пересечении.

Тогда в первом круге всего a + c точек, а во втором — c + b. Нужно найти общее число точек. В наших обозначениях это a + c + b. Чтобы можно было вычислить это выражение, его нужно записать только через известные величины a + c = 190, c + b = 230, c = 70. В искомом выражении есть a и b, которые в известных встречаются только в a + c и b + c соответственно. Значит, a + c и b + c нужно включить в запись. Однако (a + c) + (b + c) не равно a + c + b. Чтобы сравнять их, нужно отнять c. Таким образом, получаем формулу для решения задачи, в которую остаётся только подставить конкретные числа:
a + c + b = (a + c) + (b + c) − c = 190 + 230 − 70 = 350.

2.

Восьмого марта в кино пришло 100 ребят. На приключенческий фильм было продано 87 билетов, а на комедию — 63. Сколько ребят посмотрели и тот фильм, и другой? (Каждый посмотрел по меньшей мере один из фильмов.)

Указание Указание 2 Ответ

Указание. Эту и последующие задачи можно решить с помощью кругов Эйлера, подобных тем, что были в первой задаче. Обозначьте ребят точками, одним из кругов — множество ребят, купивших билеты на приключенческий фильм, а вторым кругом — множество купивших билеты на комедию. В пересечении кругов будут находится точки, соответствующие ребятам, купившим билеты на оба фильма, в объединении — всем ребятам (потому что все купили хотя бы по одному билету), а точки, лежащие только в одном из кругов — купившим только по одному билету.

Указание 2. Задача аналогична предыдущей: два круга — фильмы, точки — ребята. Сложим количества точек в обоих кругах. Получим общее число точек (оно дано) плюс посчитанное лишний раз число точек в пересечении кругов которое и требовалось найти.

Ответ. 50

3.

В кондитерском отделе супермаркета посетители обычно покупают либо один торт, либо одну коробку конфет, либо один торт и одну коробку конфет. В один из дней было продано 57 тортов и 36 коробок конфет. Сколько было покупателей, если 12 человек купили и торт, и коробку конфет?

Ответ

Ответ. 81

4.

В классе 29 человек. 15 из них занимаются в музыкальном кружке, 21 — в математическом. Сколько человек посещают оба кружка, если известно, что только Вовочка не ходит ни в один из двух кружков?

Указание Ответ

Указание. Вовочку можно обозначить точкой, лежащей за пределами обоих кругов, а значит, задача решается так же, как если бы в классе было 28 человек.

Ответ. 8

5.

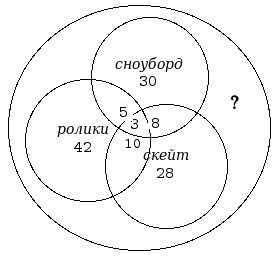
Из 100 ребят, отправляющихся в детский оздоровительный лагерь, кататься на сноуборде умеют 30 ребят, на скейтборде — 28, на роликах — 42. На скейтборде и на сноуборде умеют кататься 8 ребят, на скейтборде и на роликах — 10, на сноуборде и на роликах — 5, а на всех трех — 3. Сколько ребят не умеют кататься ни на сноуборде, ни на скейтборде, ни на роликах? (В число умеющих кататься на сноуборде включены те, кто умеет кататься ещё на чём-либо, и так далее).

Указание Указание 2 Ответ

Указание. Для иллюстрации этой задачи нужны 3 круга Эйлера; нужно найти число точек вне их всех (поскольку количество всех точек известно — всего ребят 100, то достаточно найти число точек в кругах). По сколько раз будут посчитаны точки, находящиеся в пересечении двух кругов? А трёх?

Указание 2.

Ответ. 20
Примечание: способ решения этой задачи представляет собой частный случай формулы включений-исключений для трёх множеств.

6.

Во дворе стоят машины. Некоторые из них — москвичи, а остальные — жигули. Некоторые из машин красные, а остальные белые. Некоторые из машин новые, а остальные — старые. Известно, что красных москвичей — 3, новых москвичей — 4, а новых красных машин — 5. При этом старых белых москвичей — 2, новых белых жигулей — 1, а старых красных москвичей вообще ни одного. Сколько во дворе новых красных москвичей, если всего машин 21, а старых белых жигулей — 6?

Указание Ответ Решение

Указание. Часть условия этой задачи — лишняя.

Ответ. 3

Решение. По условию, красных москвичей 3. В их число входят новые красные москвичи (число которых и нужно найти) и старые красные москвичи (по условию, их ни одного). Значит, новых красных москвичей столько же, сколько красных москвичей вообще, то есть 3.

7.

Сколько существует целых положительных чисел, меньших 100, которые:
а) делятся и на 2, и на 3;
б) делятся на 2, но не на 3;
в) делятся на 3, но не на 2;
г) делятся на 3 или на 2;
д) не делятся ни на 2, ни на 3?

Указание Указание 2 Ответ

Указание.

а) Все числа, делящиеся и на 2, и на 3, делятся на 6. Докажем это. По определению, делимость числа x на 6 означает, что x : 6 — некоторое целое число (обозначим его a), то есть что x = 6·a, где a — целое число. Аналогично, делимость на 2 означают представимость в виде x = 2·b, где b — целое, а на 3 — в виде x = 2·c с целым c. Итак, пусть x = 2·b. Так как x делится ещё и на 3, то 2·b тоже делится на 3, а раз 2 на 3 не делится, то делиться на 3 должно b, то есть b = 3·d, где d — целое. Итак, x = 2·3·d = 6·d, то есть любой x, делящийся и на 2, и на 3, делится и на 6. Значит, все нужные нам числа находятся среди делящихся на 6.
Но вдруг среди делящихся на 6 будут лишние (не делящиеся на 2 или на 3 или и на 2, и на 3 одновременно)? Докажем, что все числа, делящиеся на 6, также делятся и на 2, и на 3. Пусть x = 6·a, то есть x делится на 6. Так как 6 = 2·3, то x = 2·(3·a). Так как a — целое, то и 3·a тоже целое, а значит, x = 2·b, где b = 3·a, то есть x подходит под определение числа, делящегося на 2. Аналогично, x = 3·c, где c = 2·a, то есть x делится и на 3.
Итак, число делится и на 2, и на 3 тогда и только тогда, когда оно делится на 6. Осталось найти количество натуральных чисел, меньших 100, делящихся на 6.

Указание 2.

а) Поскольку на 6 делится каждое шестое число, то число таких чисел равно частному от деления с остатком 100 на 6 = 16 (отметим, что если бы 100 делилось на 6, то таким образом было бы найдено число таких чисел, меньших либо равных 100).

б) Нужно от числа всех делящихся на 2 (в этом промежутке) отнять число делящихся и на 2, и на 3 (уже посчитано). Останется количество чисел, делящихся на 2, но не на 3. В терминах кругов это точки, лежащие в одном круге (все, делящиеся на 2), но не лежащие во втором (делящиеся и на 2, и на 3), при этом второй круг находится полностью внутри первого, а известно количество всех точек и количество точек, лежащих во втором круге. В терминах множеств это обозначает разность множеств.

г) Первый круг обозначает точки, делящиеся на 2, а второй — на 3. Точки, лежащие в их пересечении — числа, делящиеся и на 2, и на 3 сразу (то есть делящиеся на 6). Нужно найти общее количество точек в обоих кругах, то есть в объединении множеств.

д) Количество таких чисел равно количеству всех натуральных чисел, меньших 100, минус число чисел, не удовлетворяющих условию (делящихся на 2 или на 3). Это дополнение к множеству чисел, рассматриваемому в предыдущем пункте.

Ответ. а) 16;
б) 33;
в) 17;
г) 66;
д) 34.