МАЛЫЙ МЕХМАТ МГУ

Кружок 9-11 классов

Вспомогательная раскраска 2

1.

а)

Можно ли разрезать шахматную доску на фигурки, состоящие из 4 клеток в форме буквы "т"?

б)

А можно ли разрезать на такие фигурки шахматную доску 10×10?

2.

Из шахматной доски вырезали верхнее левое и нижнее правое поля. Можно ли остаток разрезать на доминошки (дощечки 1×2)?

3.

На клетчатой плоскости в 10 соседних вертикалях сидит 10 кузнечиков — по одному на вертикали. Каждую минуту один из них прыгает в точку, симметричную ему относительно другого кузнечика. Может ли через некоторое время кузнечик Лёша оказаться на вертикали Сережи, если в начале игры они сидели на соседних вертикалях?

4.

Незнайке никак не удаётся разбить шахматную доску 6×6 на доминошки так, чтобы среди них было ровно 17 горизонтальных. Помогите ему либо доказать, что это невозможно, либо придумайте, как это сделать.

Примечание

Примечание. Шахматная раскраска тут не поможет, поскольку в шахматной раскраске любая доминошка — и горизонтальная, и вертикальная — занимает ровно одну чёрную и одну белую клетку. Так что в смысле шахматной раскраски горизонтальные и вертикальные доминошки одинаковы. Подумайте, какая раскраска лучше подойдёт для этой задачи.

5.

В трёх вершинах квадрата сидели кузнечики. Они стали играть в чехарду: один из кузнечиков прыгает в точку, симметричную относительно другого. Сможет ли хоть один кузнечик попасть в четвёртую вершину квадрата?

Примечание Указание

Примечание. Кузнечики могут прыгать за границы квадрата.

Указание. Выберите какого-то одного кузнечика и отметьте все точки, в которые он может прыгнуть.

6.

Какое наибольшее количество прямоугольников 1×4 можно вырезать из квадрата а) 6×6, б) 10×10? (Разрезы проводятся про сторонам клеток.)

7.

Какое наименьшее количество выстрелов необходимо произвести, чтобы наверняка "ранить" четырёхпалубный корабль, если поле, на котором играют, а) 8×8, б) 10×10?

8.

На шахматной доске 8×8 двое сыграли в "Морской бой" не по правилам: один расставил 21 трёхпалубный корабль, а второй выстрелил один раз и не попал. Куда он мог выстрелить? (Укажите все возможные варианты.)

9.

Докажите, что шахматную доску нельзя замостить пятнадцатью фигурками 1×4 и одним уголком из четырёх клеток.

10.

На каждой клетке доски размером 9×9 сидит жук. По свистку каждый из жуков переползает в одну из соседних по диагонали клеток. При этом в некоторых клетках может оказаться больше одного жука, а некоторые клетки окажутся незанятыми. Докажите, что при этом незанятых клеток будет не меньше девяти.

Дополнительный листок

11.

Можно ли доску размером 4×N обойти ходом коня, побывав на каждом поле ровно один раз, и вернуться на исходное поле?

12.

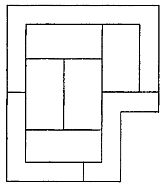Художник-авангардист хочет закончить большую абстрактную картину, изображенную на рисунке. Он решил каждую из областей окрасить только в один цвет, следя за тем, чтобы области, имеющие общую границу, не были окрашены одинаково. Площадь каждой области равна 8 квадратным футам, за исключением верхней области, имеющей вдвое большую площадь, чем остальные. Проверив запасы фломастеров, художник обнаружил, что у него осталось четыре вида фломастеров: красного фломастера у него осталось ровно столько, сколько требуется, чтобы покрыть 24 квадратных фута, желтого хватит на покрытие такой же площади, зеленого — на 16 квадратных футов и синего — на 8 квадратных футов. Может ли он закончить свою картину? А если бы у него были не фломастеры, а краски? Как ему тогда следует поступить для того, чтобы закончить свою картину?

13.

Как начертить на плоскости двухцветную карту, обладающую таким свойством, что, как бы вы ни накладывали на нее равносторонний треугольник со стороной 1, все три его вершины не должны лежать на точках одного цвета?