МАЛЫЙ МЕХМАТ МГУ

Занятие 4. Чётность, делимость, остатки

В сегодняшнем задании большинство задач (но не все) используют понятия делимости, деления с остатком, чётности. Напомним вкратце основные определения.

Говорят, что целое число a делится на целое число b, не равное нулю, если существует такое целое число c, что a = b · c. В этом случае число a называется кратным числа b, а число b — делителем числа а. Число 0 делится на любое число, любое же целое число, кроме нуля, имеет лишь конечное количество делителей.

Пусть даны целое число a и натуральное число b. Разделить число a на b с остатком — значит найти такие целые числа q и r, что 0 ≤ r < b и a = bq + r. Такая пара чисел всегда существует и единственна. Число q называют частным, а r — остатком от деления a на b. Остаток от деления числа a на b равен нулю тогда и только тогда, когда a делится на b.

Числа, дающие при делении на 2 остаток 0, называют чётными, а остаток 1 — нечётными.

Остаток от деления числа на 10 равен последней цифре десятичной записи этого числа.

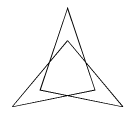Упражнение. Разделите число –1 на 1999 с остатком (то есть найдите частное и остаток).

Решение задачи 5 занятия 3. а) Ответ: да. На рисунке изображена замкнутая ломаная, удовлетворяющая условиям. (Незамкнутую ломаную нарисуйте сами.)
б) Ответ: нет. Найдём, чему может равняться количество точек самопересечения такой ломаной. Так как каждая точка самопересечения принадлежит двум звеньям, то количество этих точек должно быть вдвое меньше количества звеньев. Но число 9 нечётное, поэтому искомое количество не может равняться никакому целому числу. Значит, такой ломаной не существует.

1.	Докажите, что количество людей, живущих и когда либо живших на Земле, совершивших нечётное количество рукопожатий, чётно.
2.	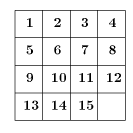Поле для «пятнашек» представляет собой коробочку размером 4×4, в которой находятся 15 фишек (квадратиков 1×1), пронумерованных числами от 1 до 15; при этом одно поле остаётся пустым. В начале игры пустое поле находилось в правом нижнем углу. Я начал двигать фишки по полю. За один ход я передвигал на пустое поле одну из фишек, находившуюся на соседнем поле. В результате порядок расположения фишек изменился, но пустое поле вновь оказалось в правом нижнем углу. Докажите, что я сделал чётное число ходов.
3.	Решите в целых положительных числах уравнения а) x² - y² = 1998; б) x² - y² = 1999. Примечание. Решить уравнение — значит найти все значения неизвестных (в случае двух неизвестных — все пары), удовлетворяющие уравнению, и доказать, что других нет.
4.	В Советском Союзе находились в обращении денежные купюры в 1, 3, 5, 10 и 25, 50 и 100 рублей. Леонид Ильич захотел разменять 25 рублей на купюры достоинством менее 10 рублей так, чтобы всего получилось 10 купюр. Удалось ли ему это сделать?
5.	На доске выписаны числа 1, 2, 3, 4, 5 и 6. Разрешается одновременно прибавлять единицу к любым двум числам. Можно ли за несколько таких операций добиться, чтобы все числа стали равными?
6.	На какую цифру оканчивается число а) 1999¹⁹⁹⁹; б) 7^{7^7⁷}?
7.	Целое число возвели в квадрат и разделили на 8. Какой остаток мог получиться?
8.	Найдите наименьшее целое положительное число, дающее при делении на 13 остаток 12, при делении на 12 остаток 11, а при делении на 11 — остаток 10.
9.	У Васи имеется шахматная доска, из которой вырезали угловые поля a1 и h8. Есть у Васи и 31 кость домино размера в две клетки шахматной доски каждая. Сможет ли Вася покрыть доминошками всю доску?
10.	Докажите, что число 8¹⁰¹ + 8¹⁰² + ... + 8¹⁰⁷ делится на 7.