МАЛЫЙ МЕХМАТ МГУ

Кружок 7 класса

Занятие 11 (5 декабря 2015 года). Его сиятельство Граф

1.

Сколькими способами можно добраться из А в Б по дорогам, изображённым на рисунках (на всех дорогах введено одностороннее движение)?

а)

б)

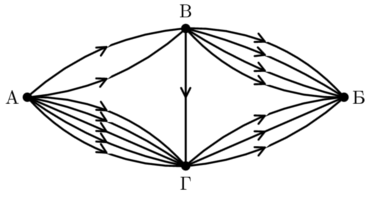
в)

2.

а)

В государстве 100 городов, и из каждого из них выходит 4 дороги. Сколько всего дорог в государстве?

б)

Может ли в государстве, где из каждого города выходит 3 дороги, быть ровно 100 дорог?

3.

В Дубках 37 домов. Можно ли протянуть телефонную сеть так, чтобы каждый дом был соединен ровно с 9 другими?

4.

Группа островов соединена мостами так, что от каждого острова можно добраться до любого другого. Турист обошёл все острова, пройдя по каждому мосту ровно один раз. На острове Восхитительный он побывал трижды. Сколько мостов ведёт с Восхитительного, если турист а) не с него начал и не на нём закончил? б) с него начал, но не на нём закончил? в) с него начал и на нём закончил?

5.

Задача Эйлера о кёнигсбергских мостах. Город Кёнигсберг (ныне Калининград) был расположен на берегах реки Прегель и двух островах, которые соединены семью мостами (на рисунке справа). Можно ли было прогуляться по городу, пройдя по каждому мосту ровно один раз, так, чтобы маршрут начался и закончился на берегу?

6.

В компании из семи мальчиков каждый имеет среди остальных не менее трёх братьев. Докажите, что все семеро — братья.

Дополнительные задачи

7.

В классе 30 человек. Может ли быть так, что 9 из них имеют по 3 друга (в этом классе), 11 — по 4 друга, а 10 — по 5 друзей?

8.

В стране Цифра есть 9 городов с названиями 1, 2, 3, 4, 5, 6, 7, 8, 9. Путешественник обнаружил, что два города соединены авиалинией в том и только в том случае, если двузначное число, составленное из цифр-названий этих городов, делится на 3. Можно ли добраться из города 1 в город 9?

9.

sunproblem: а) Петя встретился с компанией из пяти человек. Докажите, что среди этих пятерых найдутся либо трое знакомых с Петей, либо трое с ним не знакомых.

б)

Докажите, что среди любых шести человек найдутся либо трое попарно знакомых, либо три человека, никакие двое из которых не знакомы между собой.

10.

Дан кусок проволоки длиной 120 см. На какое наименьшее число кусков придётся разрубить эту проволоку, чтобы из неё можно было изготовить каркас куба с ребром 10 см?