МАЛЫЙ МЕХМАТ МГУ

Лекция 1 (196) 4.10.2008

Александр Васильевич СПИВАК,

автор книг «1001 задача по математике», «Математический кружок», «Математический праздник», «Турниры математических боёв имени А.П. Савина», «Арифметика», преподаватель Малого мехмата, учитель школ №№ 1018 и 1543.

Новость об уравнении Пелля

В октябре 2008 года вышел 109-й выпуск "Библиотечки «Квант»" — вторая часть моей «Арифметики». Одна из глав этой книги — «Уравнения Пелля». Его изучали Ферма, Эйлер, Лагранж и многие другие математики. Однако самое простое и ясное доказательство основной теоремы об уравнении Пелля — теоремы о том, что для любого натурального числа d, не являющегося квадратом, существуют такие натуральные числа x и y, что x² – dy² = 1, придумано Вайлдбергером (Сидней, Австралия) в 2008 году. Это доказательство доступно восьмикласснику и проясняет известные ранее и казавшиеся сложными теоремы об уравнениях Пелля.

Лекция 2 (197) 11.10.2008

Владимир Николаевич ЧУБАРИКОВ,

профессор, исполняющий обязанности декана механико-математического факультета МГУ.

Механико-математический факультет

В рамках «Дней науки» В.Н. Чубариков выступил перед школьниками и их родителями.

Лекция 3 (198) 18.10.2008

Александр Васильевич СПИВАК,

автор книг «1001 задача по математике», «Математический кружок», «Математический праздник», «Турниры математических боёв имени А.П. Савина», «Арифметика», преподаватель Малого мехмата, учитель школ №№ 1018 и 1543.

Простых чисел бесконечно много

Одно из самых древних математических рассуждений — доказательство Евклида бесконечности множества простых чисел. Именно оно начинает книгу М. Айгнера и Г. Циглера «Лучшие доказательства со времён Евклида до наших дней».

Другое доказательство предложил Леонард Эйлер. Оно основано на том, что гармонический ряд — сумма дробей, числители которых равны 1, а в роли знаменателя по очереди выступают все натуральные числа 1, 2, 3, 4,...— стремится к бесконечности при движении вдоль натурального ряда.

Третье из рассмотренных на лекции доказательств придумал Пауль Эрдёш. Оно основано на разложении каждого натурального числа в произведение квадрата натурального числа и числа, не делящегося на квадрат ни одного из простых чисел. Прелесть этого доказательства в том, что из него следует расходимость ряда чисел, обратных простым.

Лекция 4 (199) 25.10.2008

Сергей Борисович РЫЖИКОВ,

доцент физического факультета МГУ, секретарь оргкомитета Московской городской олимпиады по физике, учитель лицея «Вторая школа» и школы №179.

Численное моделирование и эксперименты при решении сложных задач механики

Существует легенда, что в 1590 году Галилео Галилей бросил с Пизанской башни пушечное ядро и мушкетную пулю. Хотя разница масс ядра и пули огромна, они якобы упали одновременно, опровергнув утверждение Аристотеля о том, что скорость падения тела пропорциональна его весу.

Действительно ли пуля и ядро упали одновременно? Разве воздух не оказывает сопротивление движению?

Конечно, оказывает! Но можно ли рассчитать движение, не пренебрегая сопротивлением воздуха? Решение такого рода задач механики довольно сложно, поэтому их редко рассматривают на уроках в школе. Между тем эти и им подобные задачи могут быть решены при помощи численного моделирования.

Замечательно, что при помощи довольно простых алгоритмов удаётся решать весьма сложные задачи механики. Даже нет необходимости уметь программировать: эти алгоритмы легко реализовать в программе MS Excel (или её аналоге в Open Office). Проверить расчёты можно с помощью простых экспериментов, не требующих специального оборудования.

Подробнее о численном моделировании можно прочитать в книге: С.Б. Рыжикова «Классический опыт Галилея в век цифровой техники» (издательство МЦНМО, 2008 год).

Лекция 5 (200) 1.11.2008

Светлана Анатольевна БУРЛАК,

кандидат филологических наук, старший научный сотрудник Института востоковедения РАН и филологического факультета МГУ, член оргкомитета Московской олимпиады по лингвистике и математике, автор многих олимпиадных задач по лингвистике.

Лингвистика и лингвистические задачи

16 ноября 2008 года — первый тур XXXIX Традиционной олимпиады по лингвистике. Лингвистика — наука о том, как устроены язык вообще и разные языки в частности. Она изучает языки как системы, их правила и законы: правила орфографии можно нарушить, а законы языка — нельзя. Например, почему в русском языке 6 падежей, в венгерском 16 (или даже 22), в арчинском — более 30, в английском 2, а в китайском вовсе нет? Как арчинцы справляются, а китайцы обходятся? Почему коровий и совиный, но не совий и коровиный? Почему «Отец похвалил сына и улыбнулся» по-русски понимается так, что улыбнулся отец (а не сын или, например, присутствовавший при этом дедушка)? А в других языках может быть понято так, что улыбнулся сын... Или по ситуации.

Лингвистику не «проходят» в школе, поэтому на олимпиаде мы не требуем от школьников каких-то специальных знаний. Задачи cамодостаточны: всё необходимое для решения есть в условии, то есть при помощи логических рассуждений можно понять, как устроен тот или иной фрагмент совершенно незнакомого языка, и даже перевести с него несколько слов или предложений, понять, как устроена незнакомая система письма или система счисления. Многие приемы решения задач лингвистической олимпиады, по сути, математические. Поэтому ребята, способные к математике, часто завоевывают на олимпиаде призы.

Были приведены примеры лингвистических задач и продемонстрированы математические методы, полезные для их решения. Типов задач много, на лекции были разобраны первые четыре задачи из списка.

Лекция 6 (201) 8.11.2008

Андрей Михайлович РАЙГОРОДСКИЙ,

доктор физико-математических наук, доцент кафедры математической статистики механико-математического факультета МГУ, профессор кафедры «Анализ данных» факультета инноваций и высоких технологий МФТИ, руководитель исследовательской лаборатории Яндекса.

Случайные графы

Что такое граф, известно, конечно, многим из вас. Разумеется, речь идет не о титуле, а о замечательном математическом объекте, который, удивительным образом, возникает в связи самыми разными задачами. Тут и знаменитая проблема четырёх красок, и несколько менее старая, но от этого ничуть не менее интригующая задача раскраски плоскости, и многие другие. Важность изучения свойств графов не вызывает никаких сомнений.

А если к слову граф мы добавим загадочный эпитет «случайный» ... что получится? Графы на нас с неба повалятся? Речь явно о чём-то другом ... на лекции было рассказано, о чём!

Под руководством А.М. Райгородского работала зимняя школа около Судиславля, на которой это подробно изучали.

Лекция 7 (202) 15.11.2008

Алексей Геннадьевич МЯКИШЕВ,

учитель геометрии лицея 1303, автор брошюры «Элементы геометрии треугольника» и статьи «О некоторых преобразованиях, связанных с треугольником» («Математическое образование», номер 1 (8) за 1999 год).

Окружность Конвея

В 1998 году Дж. Конвей заметил, что если для вершин A, B и C треугольника построить такие точки A', A'', B', B'', C' и C'', что точка A лежит на отрезках A'B и A''C, точка B лежит на отрезках B'C и B''A, а точка C лежит на отрезках C'A и C''B, причём AA' = AA'' = BC, BB' = BB'' = CA и CC' = CC'' = AB, то точки A', A'', B', B'', C' и C'' лежат на одной окружности — окружности Конвея. Её центр совпадает с центром вписанной окружности треугольника ABC, а квадрат её радиуса равен сумме квадратов полупериметра и радиуса вписанной окружности.

Лекция посвящена обсуждению формулировки этой теоремы Конвея и варианта его конструкции, когда вместо приведённых выше равенств рассматриваем равенства AA'' = BB' = AB, BB'' = CC' = BC и CC'' = AA' = CA. При помощи программы «Живая геометрия» изготовлены убедительные чертежи, демонстрирующие окружность, проходящую через все шесть центров описанных окружностей треугольников, на которые разбивают произвольный треугольник его медианы, и открытую Я.&nbssp;Ганиным прямую Эйлера четырёхугольника.

Подробную статью можно прочитать на сайте А.Г. Мякишева.

Лекция 8 (203) 22.11.2008

Алексей Александрович ЗАСЛАВСКИЙ,

старший научный сотрудник ЦЭМИ РАН, председатель жюри олимпиады по геометрии им. И.Ф.Шарыгина, автор книг «Геометрические преобразования» (МЦНМО, 2003), «Геометрические олимпиады имени И.Ф. Шарыгина» (в соавторстве с В.Ю. Протасовым и Д.И. Шарыгиным), «Геометрические свойства кривых второго порядка» (в соавторстве с А.В. Акопяном), член редколлегии журнала «Квант».

Гипербола Кипера

Если построить на сторонах треугольника ABC как наоснованиях подобные равнобедренные треугольники ABC', BCA', CAB', то прямые AA', BB', CC' пересекутся в одной точке. Геометрическое место таких точек — гипербола, проходящая через вершины, центр тяжести и ортоцентр (точку пересечения высот) треугольника. Будет приведено геометрическое доказательство этого факта, ранее, видимо, неизвестное, и доказан ряд красивых свойств этой гиперболы.

Иллюстрацию, выполненную в программе «Живая геометрия», можно анимировать, двигая по пунктирной прямой лежащую на ней точку.

Помимо школьной программы, слушатели должны знать основные понятия и теоремы проективной геометрии.

Лекция 9 (204) 29.11.2008

Александр Васильевич СПИВАК,

автор книг «1001 задача по математике», «Математический кружок», «Математический праздник», «Турниры математических боёв имени А.П. Савина», «Арифметика», преподаватель Малого мехмата, учитель школ №№ 1018 и 1543.

Разбиения чисел на слагаемые

Количество разбиений числа на нечётные слагаемые равно количеству разбиений на попарно различные слагаемые. Этот факт был доказан как при помощи явного указания биекции, так и при помощи бесконечных рядов — производящих функций.

Лекция 10 (205) 6.12.2008

Евгений Дмитриевич КУЛАНИН,

кандидат физико-математических наук, профессор факультета информационных технологий МГППУ, автор учебника и задачника по геометрии для 10-11 классов (Айрис-пресс, 1997), сборника «3000 конкурсных задач по математике» (Айрис-пресс, 2007 год) и статей «Об одной трудной геометрической задаче» (седьмой номер «Кванта» 1992 года), «Об описанных окружностях чевианных и педальных треугольников и некоторых кривых, связанных с треугольником» (Девятый номер ежегодника «Математическое просвещение», 2005 год), «О прямых Симсона, кривой Штейнера и кубике Мак-Кэя» («Математическое просвещение», 2006 год), «Виктор Тебо и его задачи» («Математическое просвещение», 2007 год) и других статей и задач по элементарной геометрии, опубликованных на русском, английском, немецком, датском, болгарском и румынском языках.

Точки Фейербаха и Тебо

На описанной окружности разностороннего треугольника существуют такие четыре точки, что наибольшее расстояние от такой точки до вершин треугольника равно сумме расстояний от неё до двух оставшихся вершин треугольника. Эти точки совпадают с точками Фейербаха треугольника, середины сторон которого совпадают с вершинами данного треугольника и с точками Тебо треугольника, основания высот которого совпадают с вершинами данного треугольника.

Приведём более подробные пояснения. Пусть АН₁, ВН₂, СН₃ — высоты непрямоугольного треугольника АВС. Тогда прямые Эйлера треугольников АН₂Н₃, ВН₃Н₁, СН₁Н₂ пересекаются в такой точке Т окружности Эйлера треугольника АВС, для которой длина одного из отрезков ТН₁, ТН₂ и ТН₃ равна сумме длин двух остальных. Точку T называют точкой Тебо треугольника АВС. Обозначим точку пересечения высот остроугольного треугольника АВС буквой Н. Обозначим через Т, T_a, T_b и T_c точки Тебо треугольников АВС, ВСН, САН и АВН соответственно.

Согласно знаменитой теореме Фейербаха окружность девяти точек данного треугольника касается вписанной и трех вневписанных окружностей этого треугольника. Точку касания окружности девяти точек с вписанной окружностью называют внутренней точкой Фейербаха, а точки касания с вневписанными окружностями — внешними точками Фейербаха. Теперь можно сформулировать основной результат лекции.

Пусть Н — ортоцентр остроугольного разностороннего треугольника АВС, Н₁, Н₂, Н₃ — основания его высот; Н'₁Н'₂Н'₃ — треугольник, серединный треугольник которого совпадает с треугольником Н₁Н₂Н₃. Тогда точки Тебо Т, T_a, T_b и T_c треугольников АВС, ВНС, СНА и АНВ соответственно совпадают с точками Фейербаха треугольника Н'₁Н'₂Н'₃, причём точка T совпадает с внутренней, а точки T_a, T_b и T_c — c внешними точками Фейербаха треугольника Н'₁Н'₂Н'₃.

Советую ознакомиться с иллюстрацией в программе «Живая геометрия».

Лекция 11 (206) 13.12.2008

Владимир Юрьевич ПРОТАСОВ,

доктор физико-математических наук, профессор механико-математического факультета МГУ, член редколлегии журнала «Квант», автор задач, предлагавшихся на Всероссийской, Соросовской, Московской олимпиадах, Турнире городов, геометрической олимпиаде имени И.Ф. Шарыгина, один из организаторов геометрической олимпиады имени И.Ф. Шарыгина и cеминара по геометрии в Независимом математическом университете, автор брошюры «Максимумы и минимумы в геометрии» (Библиотека «Математическое просвещение», издательство МЦНМО, 2005 год, 56 страниц), соавтор (с А.А. Заславским и Д.И. Шарыгиным) книг «Геометрические олимпиады имени И.Ф. Шарыгина» (издательство МЦНМО, 2007 год, 152 страницы) и «Игорь Федорович Шарыгин. К семидесятилетию со дня рождения» (издательство МЦНМО, 2007 год, 304 страницы), автор статей «Вокруг теоремы Фейербаха» («Квант», девятый номер 1992 года), соавтор (с И.Ф. Шарыгиным) статьи «Нужна ли школе XXI века геометрия?» («Очерки по истории образования в России», издательство МГУ, 2004 год), соавтор (с В.М. Тихомировым) статьи «Геометрические шедевры И.Ф. Шарыгина» («Квант», первый номер 2006 года), соавтор (с Я. Бринкхаусом) статьи «Теория экстремума в простых примерах» («Математическое просвещение», выпуск 9, 2004 год), автор статьи «Об одном обобщении теоремы Понселе» (Успехи Математических наук, 2007, номер 6), автор статей «О двух велосипедистах и вишневой косточке» («Квант», третий номер 2008 года), «Касающиеся окружности: от Тебо до Фейербаха» («Квант», четвёртый номер 2008 года).

От Тебо до Фейербаха

В четвёртом номере «Кванта» 2008 года опубликована статья, в которой изложены красивые доказательства двух трудных теорем: теоремы Тебо и теоремы Фейербаха. Слушатели узнали, что это за теоремы и как можно их доказать.

Лекция 12 (207) 14.02.2009

Александр Васильевич СПИВАК,

автор книг «Математический праздник», «Турниры математических боёв имени А.П. Савина», «Арифметика» и «Арифметика-2», учитель школ №№ 1018 и 1543.

Что такое высшая математика?

Иногда творчески относящиеся к своей работе чиновники министерства образования Российской Федерации задумываются, нельзя ли прекратить знакомство школьников с идеями высшей математики. Что же это такое — высшая математика? Чем она отличается от математики постоянных величин, когда и кем была создана? Бывает ли математика средней? Низкой? Что такое элементарное и неэлементарное доказательство?

Перечислить всех создателей высшей математики невозможно, поэтому было рассказано только о двух её творцах — об Архимеде, вычислявшем интегралы, и об Иоганне Кеплере (1571–1630), издавшем в 1615 году книгу «Новая стереометрия винных бочек, преимущественно австрийских, как имеющих самую выгодную форму и исключительно удобное употребление для них кубической линейки», в которой он сформулировал правило отыскания наибольшего значений функции.

Возврат к математике постоянных величин затруднителен по той же причине, по какой трудно уговорить нынешних школьников добровольно отказаться носить ботинки и надеть вместо них лапти: изгнав производные из курса математики, сразу обнаружите их в физике (скорость и ускорение!), а запретив интегрировать, вдруг выясните, что заодно разучились вычислять площади, длины, объёмы и почти все другие величины. Слушатели убедились, что их креативность на лекции 14.02.2009 не пострадала.

Лекция 13 (208) 21.02.2009

Владимир Георгиевич СУРДИН,

кандидат физико-математических наук, старший научный сотрудник ГАИШ МГУ.

Приливные силы на Земле и в космосе

Среди четырех фундаментальных сил природы — гравитационной, электромагнитной, сильной и слабой ядерных,— этой силы нет. Тем не менее, вызванные приливной силой эффекты влияют на движение планет, звёзд и галактик, расположение созвездий, на погоду, морскую и речную навигацию, на рост растений и эволюцию биосферы. Даже идея создания машины времени, которую можно было бы осуществить, используя чёрные дыры, наталкивается на почти непреодолимое препятствие — приливные силы. Впрочем, поняв их особенности, вы, возможно, сумеете преодолеть и это!

Эта лекция уже была прочитана на лектории МММФ 1.12.2001; вышла брошюра: В.Г. Сурдин, «Пятая сила», выпуск 17 серии «Библиотека "Математическое просвещение"».

Лекция 14 (209) 28.02.2009

Александр Васильевич СПИВАК,

автор книг «Математический праздник», «Турниры математических боёв имени А.П. Савина», «Арифметика» и «Арифметика-2», учитель школ №№ 1018 и 1543.

Натуральный логарифм и экспонента

Идеи высшей математики, как убеждён министр Фурсенко, убивают креативность. Что это за идеи? В частности, что такое логарифм? Что такое число e и почему оно столь же важно, как и число π? Как связана площадь под графиком функции y = 1 / x с операцией логарифмирования? Слушатели убедились, что их креативность на лекции 28.02.2009 не пострадала.

Лекция 15 (210) 7.03.2009

Александр Васильевич СПИВАК,

автор книг «Математический праздник», «Турниры математических боёв имени А.П. Савина», «Арифметика» и «Арифметика-2», учитель школ №№ 1018 и 1543.

Максимумы и минимумы

Это третья лекция об идеях высшей математики, которые, как убеждён министр Фурсенко, убивают креативность. Что это за идеи? Какие задачи можно решать элементарными методами, а где нужно уметь дифференцировать? Какие свойства функций можно изучить элементарными методами, а какие — методами высшей математики?

Как и после первых двух лекций цикла, слушатели сами поняли, что их креативность на лекции 7.03.2009 не пострадала.

Лекция 16 (211) 14.03.2009

Александр Васильевич СПИВАК,

автор книг «Математический праздник», «Турниры математических боёв имени А.П. Савина», «Арифметика» и «Арифметика-2», учитель школ №№ 1018 и 1543.

Ряды и дифференциальные уравнения

Это четвёртая лекция об идеях высшей математики, которые, как убеждён министр Фурсенко, убивают креативность. Что это за идеи? Какие задачи можно решать элементарными методами, а где нужно уметь дифференцировать? Какие свойства функций можно изучить элементарными методами, а какие — методами высшей математики?

Как и после первых трёх лекций цикла, слушатели поняли, что их креативность не пострадала.

Лекция 17 (212) 21.03.2009

Игорь Анатольевич ШЕЙПАК,

доцент кафедры теории функций и функционального анализа мехмата МГУ.

Фракталы: самоподобные множества и самоподобные функции

Будет рассказано об удивительных множествах — фракталах. Наивное определение фрактала заключается в том, что некоторая часть фигуры похожа на всю фигуру в целом.

Первые примеры таких объектов были построены на рубеже XIX-XX веков, но систематическое изучение их началось только в шестидесятые годы прошлого века. Тогда же и возник и сам термин «фрактал». Развитие компьютерной техники стимулировало изучение фракталов и подняло его на новый уровень.

Строгого определения, что такое фрактал, нет до сих пор. Тем не менее математики придумали некоторые характеристики, позволяющие выделить основные особенности фрактала. На лекции будут рассмотрены две из них: фрактальная и аппроксимативная размерности. У «обычных» фигур (например, отрезка, квадрата) эти размерности обязательно целые (у отрезка и квадрата — 1 и 2 соответственно). Фигуры, которые сейчас принято считать «классическими» фракталами (например, совершенное множество Кантора, треугольник Серпинского, снежинка Нильса Фабиана Хельге фон Коха), имеют всегда дробную размерность.

Оказывается, многие фракталы являются «неподвижными точками» некоторого сжимающего отображения. Получающиеся фракталы называют аффинно-самоподобными. Фракталы этого класса являются частным случаем более широкого класса самоподобных множеств. Самоподобные функции — это те функции, графики которых представляют собой самоподобные множества. Будет рассказано, как их можно строить, в том числе и с помощью компьютера.

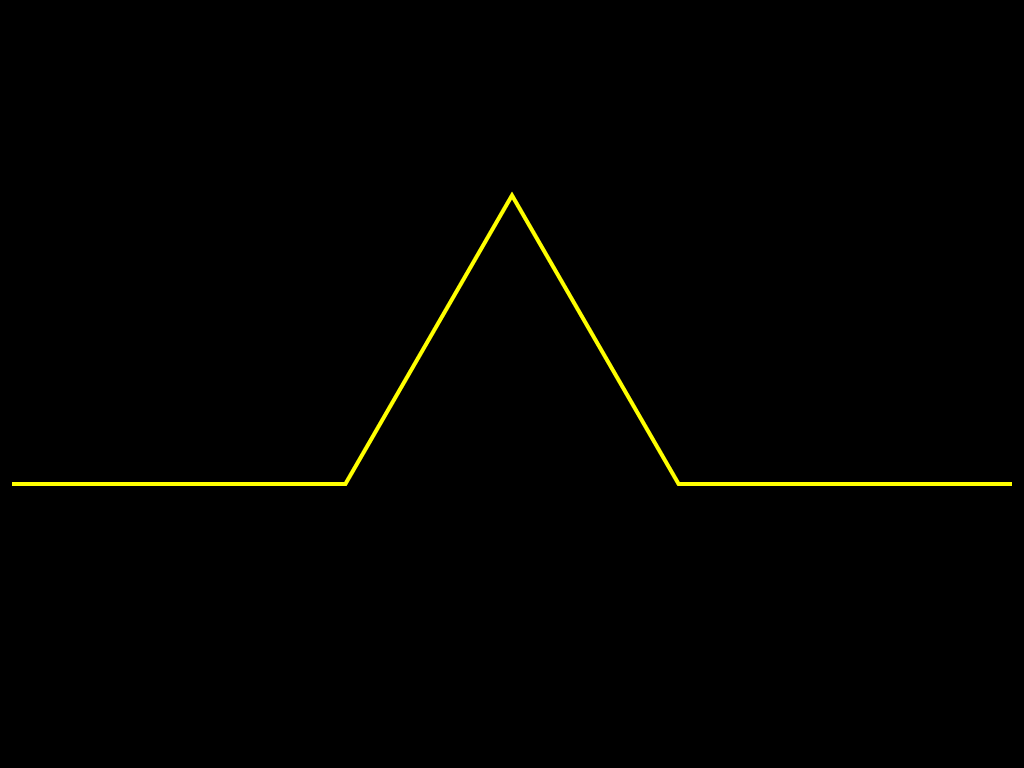
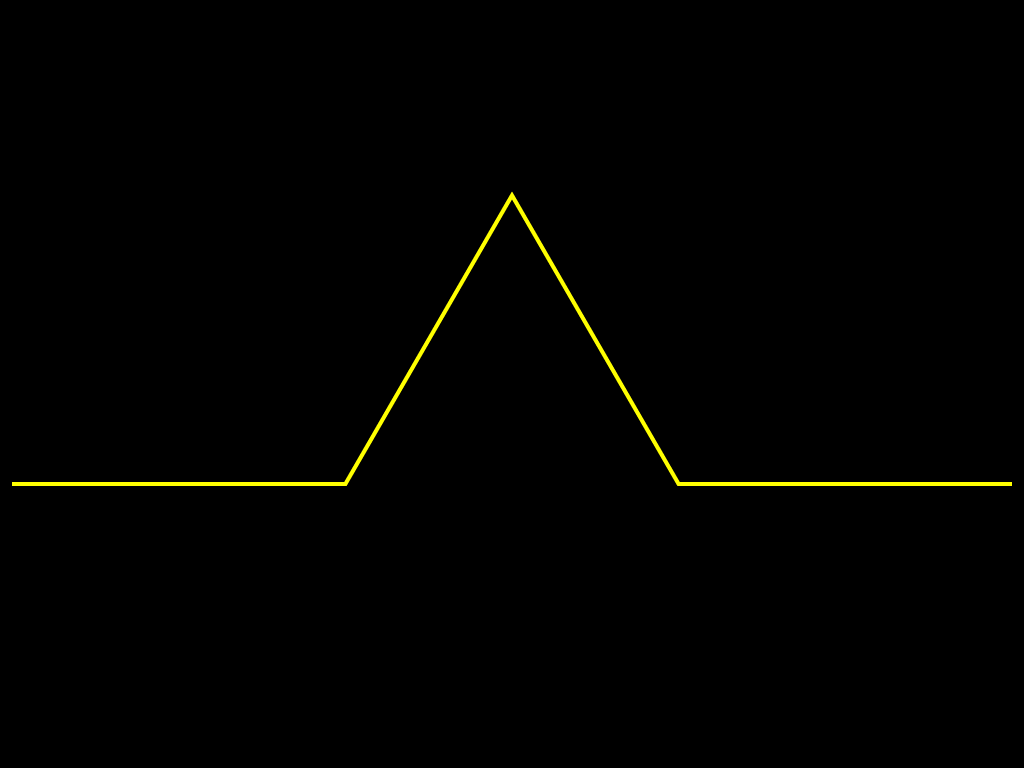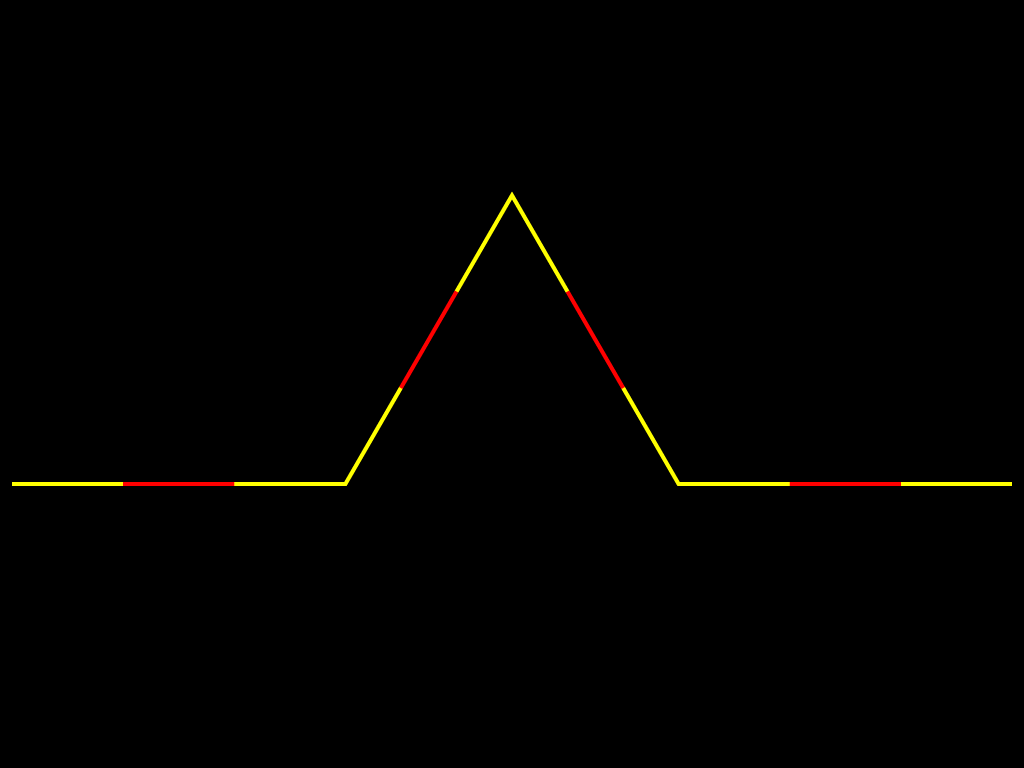
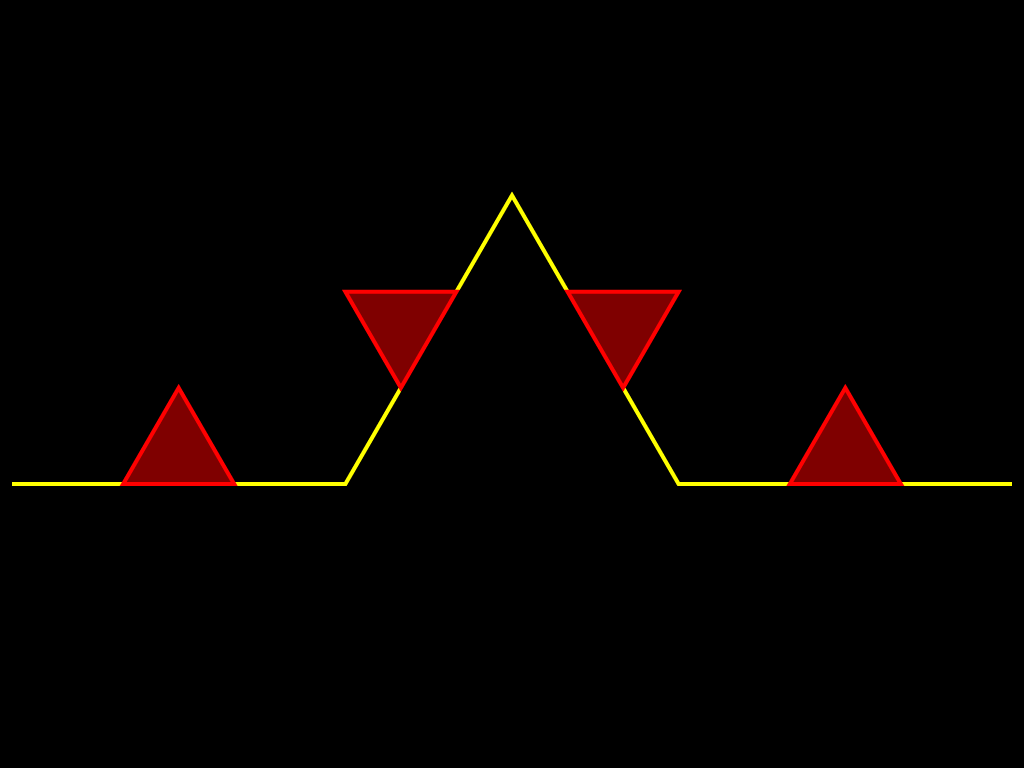
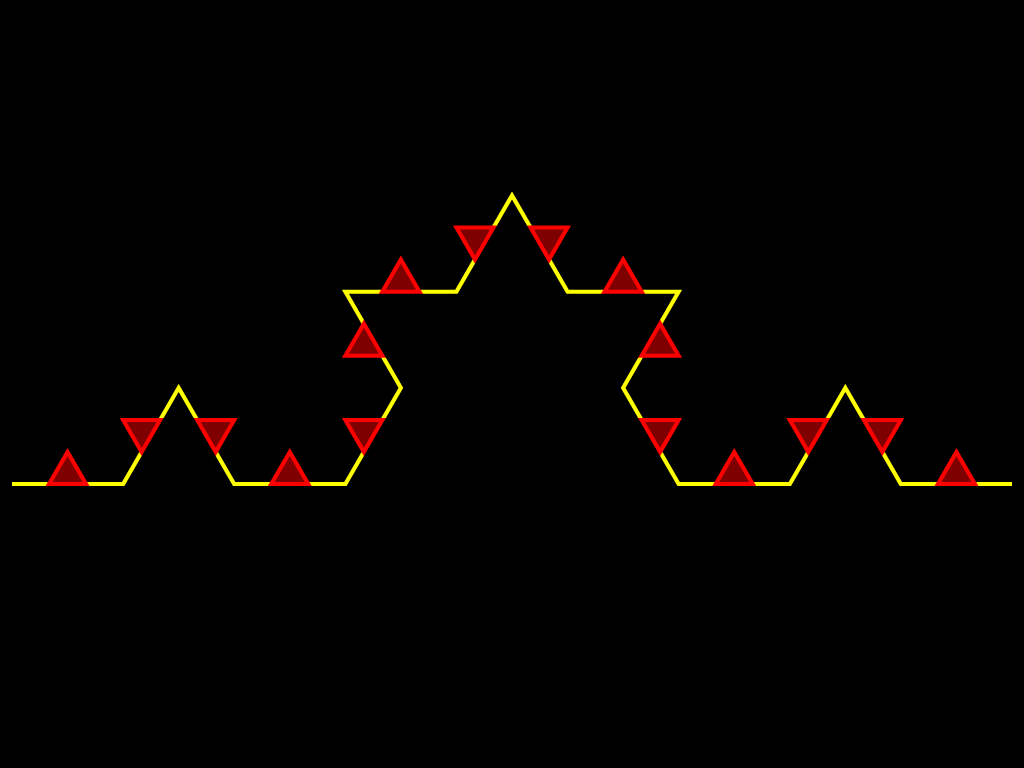
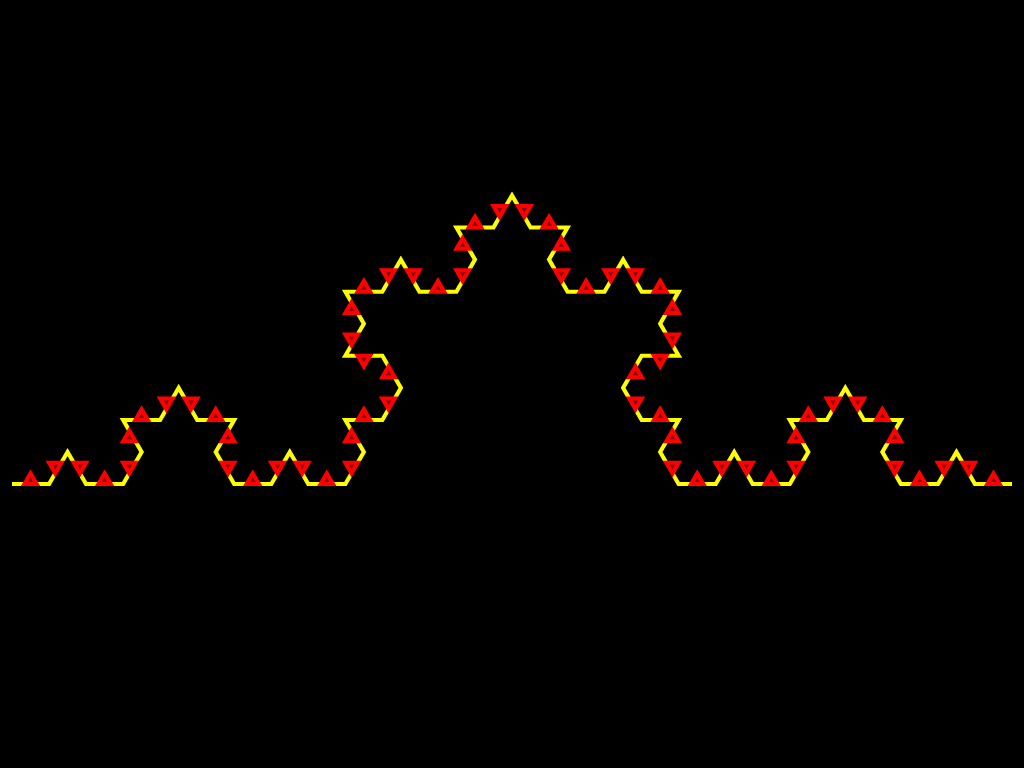
Другой класс фракталов, к которым относятся множество Мандельброта и множества Жюлиа, возникает при изучении динамики точек на комплексной плоскости. Эти множества оказали влияние не только на развитие соответствующих разделов математики, но и положили начало такому направлению искусства, как математическое искусство. Они также получили широкое применение в компьютерной графике. Вот как изобразил М.Ю. Панов процесс построения снежинки Коха:

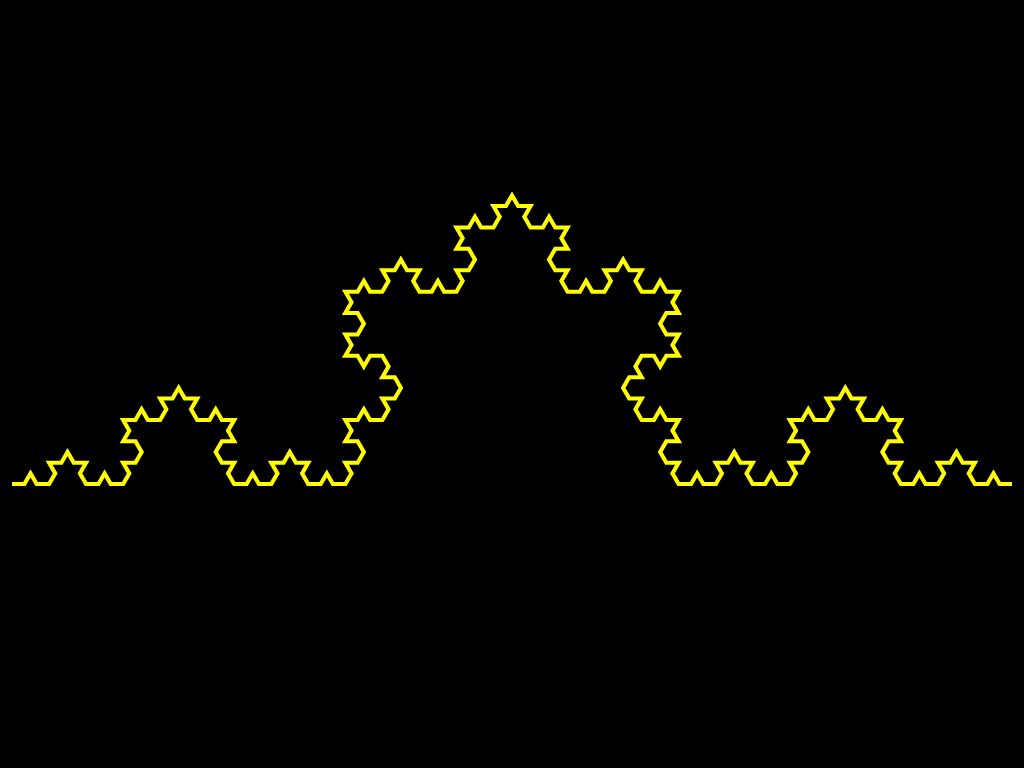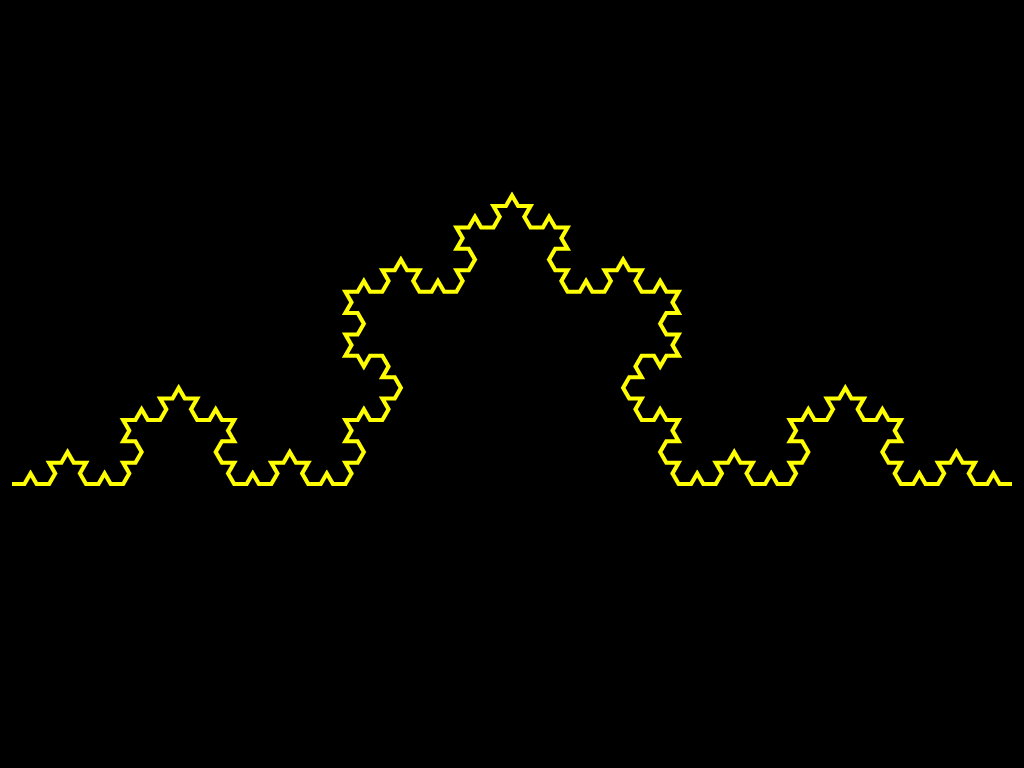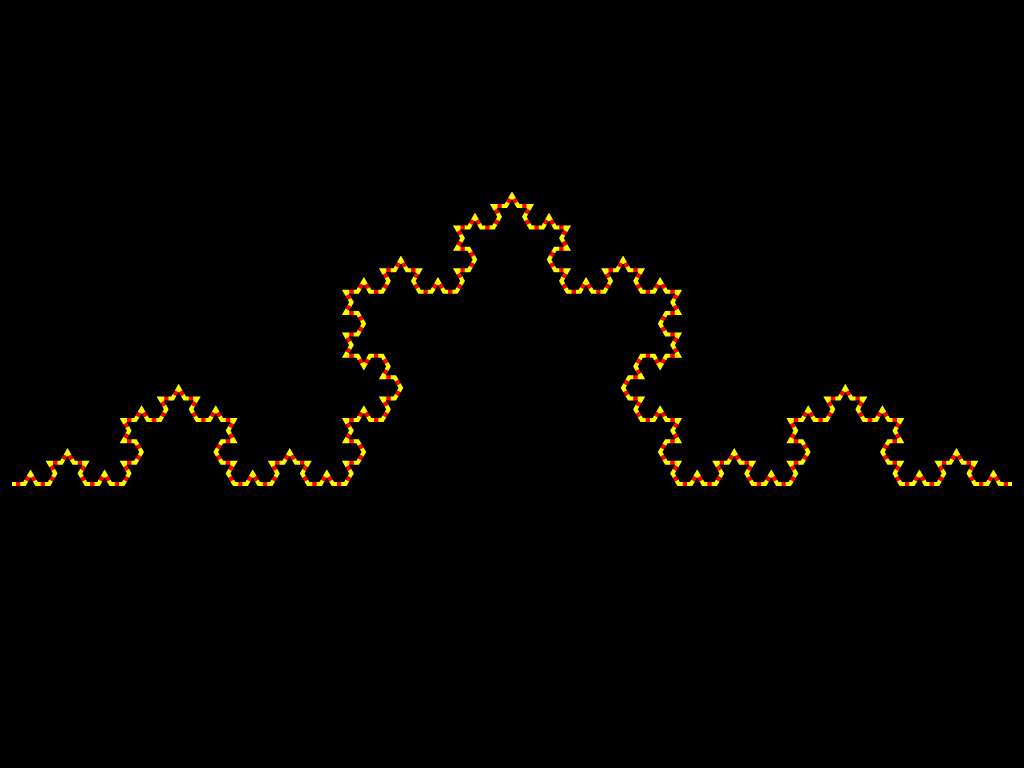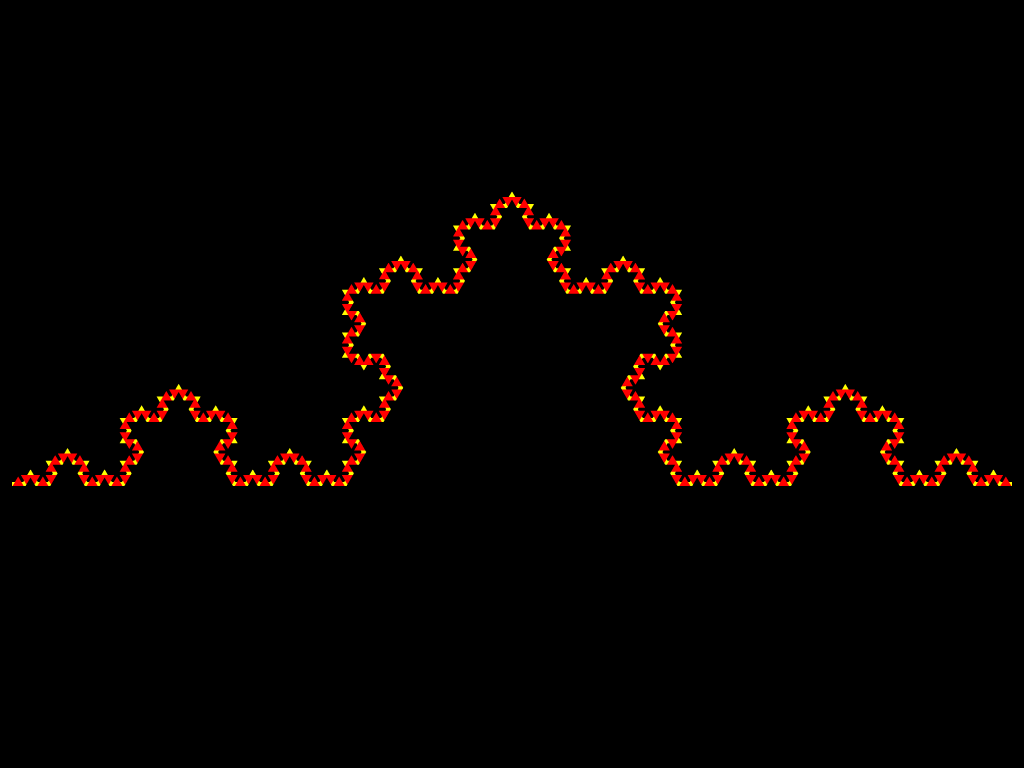Лекция 18 (213) 28.03.2009

Александр Васильевич СПИВАК,

автор книг «Математический праздник», «Турниры математических боёв имени А.П. Савина», «Арифметика» и «Арифметика-2», учитель школ №№ 1018 и 1543.

Огибающие семейств прямых, эволюты и эвольвенты

Это пятая лекция об идеях высшей математики, которые, как убеждён министр Фурсенко, убивают креативность. Что это за идеи? Какие задачи можно решать элементарными методами, а где нужно уметь дифференцировать? Какие свойства функций можно изучить элементарными методами, а какие — методами высшей математики?

Как и после первых четырёх лекций цикла, слушатели поняли, что их креативность не пострадала.

Лекция 19 (214) 11.04.2009

Андрей Михайлович РАЙГОРОДСКИЙ,

доктор физико-математических наук, доцент МГУ, профессор МФТИ, руководитель исследовательской лаборатории Яндекса, учитель школы 179

Эрдёш и Секереш: задача о выпуклых многоугольниках

В каждом ли множестве из трёх или более точек плоскости есть вершины треугольника? Вообще-то, нет: точки могут лежать на одной прямой. Скажем, что точки находятся в общем положении, если никакие три из них не лежат на одной прямой. Для множества точек общего положения ответ на поставленный вопрос, конечно, утвердительный. А если мы станем искать выпуклые четырёхугольники? Понятно, что трёх точек не хватит. Не хватит и четырёх точек (одна точка может лежать внутри треугольника с вершинами в других трёх точках), а вот пяти точек общего положения уже достаточно. Этот факт в 1934 году доказала Эстер Кляйн. Сейчас известно, что среди любых 9 точек общего положения есть вершины выпуклого пятиугольника, а среди любых 17 точек общего положения есть вершины выпуклого шестиугольника.

За прошедшие с тех пор три четверти века из наблюдения Кляйн вырос целый раздел комбинаторной геометрии — раздел, полный интересных, важных и зачастую по-прежнему нерешённых проблем. Им посвящена статья В. Кошелева и А. Райгородского «Задача Эрдёша–Секереша о выпуклых многоугольниках» второго номера «Кванта» 2009 года, часть содержания которой, в том числе романтическая история, была изложена на лекции.

Лекция 20 (215) 18.04.2009

Дмитрий Викторович ШВЕЦОВ,

студент четвёртого курса математического факультета Московского государственного педагогического университета, учитель школы № 179.

От прямой Симсона до теоремы Дроз-Фарни

Основания перпендикуляров, опущенных из точки описанной окружности треугольника на его стороны или их продолжения, лежат на одной прямой — прямой Симсона. Эта и другие красивые теоремы были доказаны на лекции. Её расширенный текст опубликован в шестом номере «Кванта» 2009 года.

Лекция 21 (216) 25.04.2009

Алексей Львович ГОРОДЕНЦЕВ,

профессор Независимого московского университета и кафедры алгебры математического факультета Высшей школы экономики, старший научный сотрудник Института теоретической и экспериментальной физики.

Формальные степенные ряды и вычисления сумм

Суммы первых нескольких натуральных чисел, сумма их квадратов, кубов, четвёртых степеней можно вычислять разными способами. Один из этих способов использует степенные ряды. Он и был рассказан на лекции.

Лекция 22 (217) 2.05.2009

Дмитрий Викторович ШВЕЦОВ,

студент четвёртого курса математического факультета Московского государственного педагогического университета, учитель школы № 179.

Капризы биссектрис

Какие свойства медиан и высот треугольника верны для его биссектрис, а какие нет? Например, следует ли из равенства длин двух биссектрис треугольника, что он равнобедренный?Этот и многие другие вопросы были обсуждены на лекции.

Лекция 23 (218) 16.05.2009

Сергей Константинович ЛАНДО,

проректор Независимого Московского университета, декан факультета математики Государственного университета Высшая Школа Экономики, член правления Московского Математического Общества.

Многочлены Абеля

Последовательность многочленов A_n (x) = x (x + n)^{n - 1} обладает очень интересными свойствами. Например, она тесно связана с простейшими графами — деревьями и лесами. Точнее говоря, коэффициенты многочлена A_n перечисляют леса на n вершинах. Было рассказано и о других свойствах многочленов Абеля.