МАЛЫЙ МЕХМАТ МГУ

Кружок 6 класса

Занятие 23 (23 апреля 2016 года). Геометрия — 3

1.

Придумайте и покажите, как можно разрезать куб на три пирамиды.

2.

Из кубика Рубика 3×3×3 удалили центральный шарнир и восемь угловых кубиков. Можно ли оставшуюся фигуру из 18 кубиков составить из шести брусков размером 3×1×1?

3.

Как из семи «уголков», каждый из которых склеен из трёх кубиков 1×1×1, и шести отдельных кубиков 1×1×1 составить большой куб 3×3×3? Можно ли сделать так, чтобы все отдельные кубики оказались в серединах граней большого куба?

4.

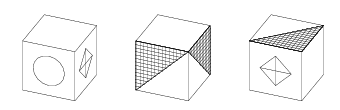
Придумайте такую раскраску граней кубика, чтобы в трёх различных положениях он выглядел так, как это показано на рисунке. (Укажите, как раскрасить невидимые грани, или нарисуйте развёртку.)

5.

На столе лежит кубик, на его верхней стороне нарисована картинка. Кубик несколько раз перекатывали по столу через ребро, после чего он вновь оказался на прежнем месте. Могло ли оказаться, что картинка повёрнута на 180 градусов по сравнению с исходным положением?

6.

Некоторые рёбра куба красные, а остальные — чёрные. При этом в каждую вершину приходит не более одного красного ребра. Какое наибольшее количество красных рёбер может быть у такого куба?

7.

В какое наименьшее количество красок можно покрасить рёбра а) куба; б) тетраэдра; в) октаэдра так, чтобы каждое ребро было покрашено одной краской и любые два ребра, имеющие общую вершину, были бы покрашены в разные цвета?

8.

Если смотреть на аквариум спереди, то рыбка проплыла, как показано на левом рисунке. А если справа — то как на правом рисунке. Нарисуйте вид сверху.