МАЛЫЙ МЕХМАТ МГУ

Кружок 7 класса

Руководитель Варвара Алексеевна Косоротова
2009/2010 учебный год

Занятие 8. Разрезания на клетчатом листе бумаги

При решении задач такого типа полезно применять следующие соображения:

  1. Площадь. Если требуется разбить фигуру на несколько равных частей, стоит сначала найти площадь разрезаемой фигуры, а потом — каждой из частей. Сходным образом, если исходную фигуру нужно разбить на несколько фигур заданного вида, стоит предварительно посчитать, сколько их должно быть. Такие же соображения могут помочь и при решении других задач на разрезание. Для иллюстрации этой идеи автор этих строк добавил в список задачу 13, которой не было среди задач, предлагавшихся на занятии.
  2. Симметрия. Свойствам симметрии следует уделять внимание, например, в случае, когда требуется разрезать одну фигуру на части и из них собрать другую фигуру.
К простым задачам приведены только ответы, к более сложным — еще и соображения, помогающие получить ответ.

1.
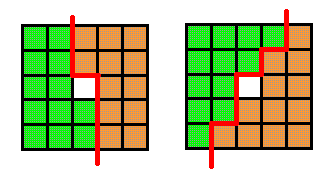
Разрежьте квадрат 5×5 с дыркой (см. рисунок) на две равные части двумя способами. Способы разрезания квадрата на две части будем считать различными, если части квадрата, полученные при одном способе разрезания, отличаются по форме или размеру от частей, полученных при другом способе (то есть их нельзя совместить наложением).

Ответ

2.
Разделите квадрат 4×4 на две равные части четырьмя различными способами так, чтобы линия разреза шла по сторонам клеток.

Ответ

3.
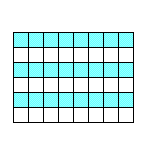
Флаг – 1. Разрежьте флаг с 6 полосами на две части так, что бы из них можно было сложить флаг с 8 полосами.

Ответ

4.
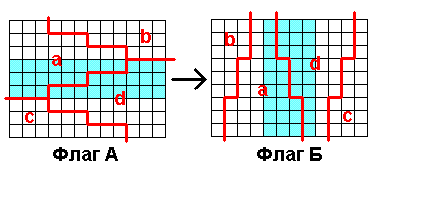
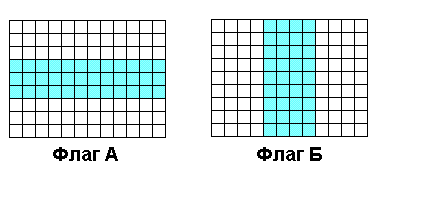
Флаг – 2. Разрежьте флаг А на четыре части так, чтобы из них можно было сложить флаг Б.

Ответ

5.
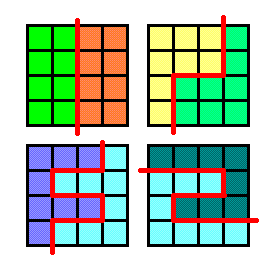
Разрежьте фигуру на 4 равные части.

Ответ

6.
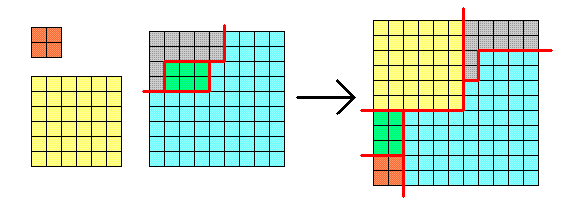
Из двух — один. Разрежьте квадрат с дыркой двумя прямыми на 4 части так, чтобы из них и еще одного обычного квадрата 5×5 можно было сложить новый квадрат.

Ответ Решение

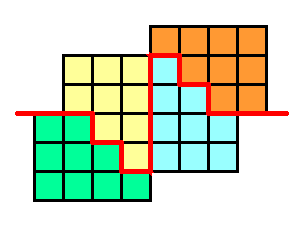
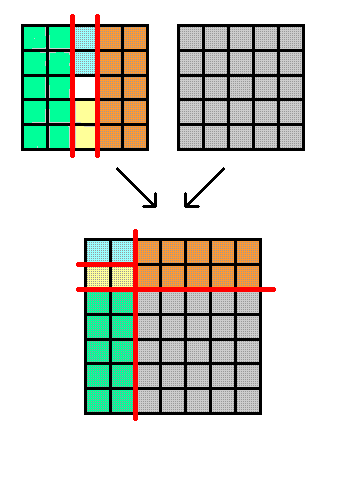
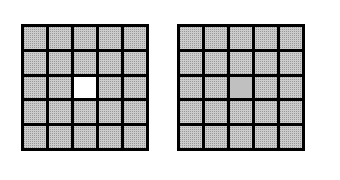Решение. Здесь стоит сначала вычислить сторону квадрата, который должен получиться. Он будет состоять из стольких же клеток, что и исходные фигуры, а их общая площадь составляет 5·5+(5·5-1)=49 клеток. 49=7², поэтому сторона квадрата равна 7 клеткам. Значит, нужно каким-то образом «нарастить» квадрат 5×5.
Разрезать квадрат с дыркой на 4 части двумя прямыми можно, только если эти прямые касаются краев дырки. Сделать это так, чтобы разрезу проходили по сторонам клеток, можно только так, как показано на рисунке (см. Ответ к этой задаче). После того, как эти рассуждения проведены, завершить решение не составит труда.
7.
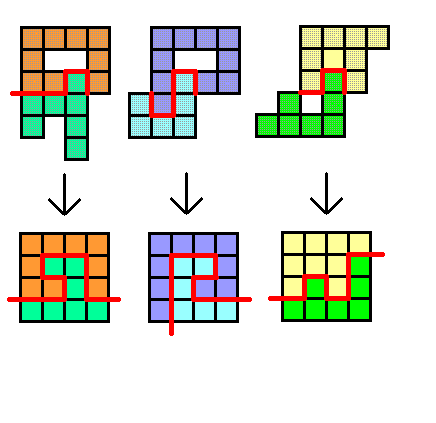
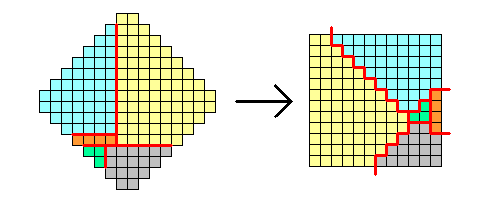
Три фигуры. Для каждой из изображенных на рисунке фигур придумайте способ разрезать ее на две части, из которых можно сложить квадрат.

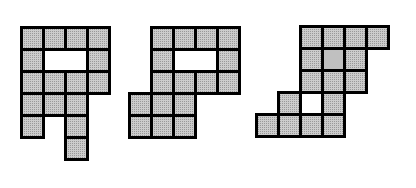
Примечание. В условиях задач, выдававшихся на занятиях, эта задача была сформулирована несколько иначе: там предлагалось разрезать любую из трех фигур на две части, из которых можно было бы собрать квадрат. Подразумевается, что предложить способ такого разрезания надо для каждой из фигур, а не только для какой-то одной.

Ответ Решение

Решение. Обратим внимание, что каждая из указанных фигур состоит из 16=4·4 клеток, значит, квадрат получится размера 4×4. Дальше надо постараться «увидеть» часть этого квадрата на рисунке и часть фигуры, которую надо отрезать и передвинуть.
8.
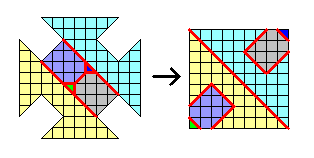
Мальтийский крест – 1. Разрежьте «мальтийский крест» (см. рисунок) на 6 частей так, чтобы из них можно было сложить квадрат.

Ответ Решение

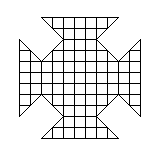Решение. В этой задаче не стоит искать сторону квадрата, который должен получиться. Лучше просто внимательно посмотреть на рисунок. У мальтийского креста 4 оси симметрии: вертикальная, горизонтальная и две диагональных (как, впрочем, и у квадрата). Обратим особое внимание на диагональную ось симметрии и постараемся делать наши разрезы симметричными относительно нее. Если провести два длинных диагональных разреза (см. рисунок в Ответе к этой задаче), «вытащить» прямоугольник, образовавшийся внутри, а оставшиеся две части сдвинуть друг к другу, получится «квадрат» с двумя «дырками» в углах. Чтобы их заполнить, надо разрезать оставшийся прямоугольник на 4 части. Это легче будет сделать, вновь принимая во внимание соображения симметрии.
9.
Из трех — один. Дано три квадрата: 2×2, 6×6 и 9×9. Разрежьте самый большой квадрат на три части так, чтобы из полученных пяти фигур можно было сложить один квадрат.

Ответ Решение

Решение. В этой задаче несложно вычислить площадь квадрата, который мы пытаемся собрать. Она равна 2·2+6·6+9·9=4+36=81=121=11², поэтому квадрат будет иметь сторону 11. Дальнейший ход решения зависит от вашего воображения. Кстати, вполне возможно, что приведенный в ответе способ разрезания — не единственный.
10.
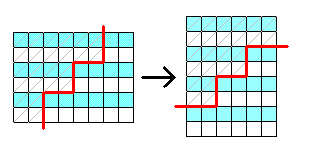
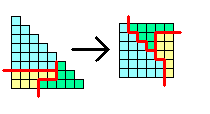
«Лесенка». Превратите «лесенку» в квадрат, разрезав ее на три части.

Ответ

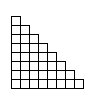
11*.
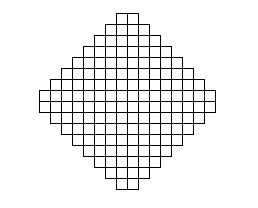
Зубчатый квадрат. Превратите зубчатый квадрат в обыкновенный, разрезав его на 5 частей.

Ответ

12*.
Мальтийский крест – 2. Разрежьте «мальтийский крест» (см. задачу 8) на 5 частей так, чтобы из них можно было сложить квадрат.

Ответ Решение

Решение. Аналогично решению задачи 8.
13**.
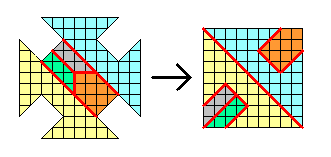
Незнайка разрезал изображенную на рисунке фигуру на трехклеточные и четырехклеточные уголки (такие, как на рисунке). Сколько каких уголков могло получиться у Незнайки? Рассмотрите все возможные случаи!

Ответ Решение

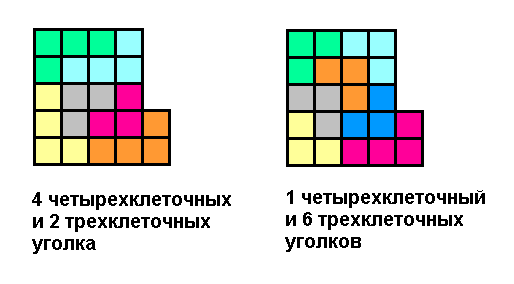
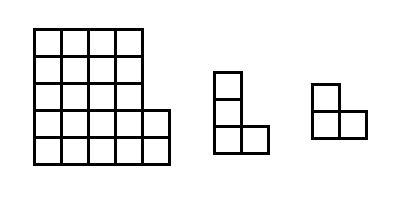Ответ. 4 четырехклеточных и 2 трехклеточных уголка либо 1 четырехклеточный и 6 трехклеточных.
Решение. Площадь исходной фигуры равна 22 (за единицу площади принимаем одну клетку). Пусть при разрезании использовано n четырехклеточных и k трехклеточных уголков. Тогда выразим площадь большой фигуры как сумму площадей уголков: 22=3k + 4n. Перепишем это равенство в таком виде: 22 − 4n=3k. В левой части этого равенства стоит четное число, которое, однако, не делится на 4. Значит, 3k — тоже четное число, не делящееся на 4, а следовательно, таковым является и само число k. Кроме того, в правой части равенства стоит число, кратное 3, поэтому 22 − 4n тоже кратно 3. Таким образом, 22 − 4n кратно 6. Перебирая значения n от 0 до 5 (при n≥6 22 − 4n<0<3k, чего быть не может), получаем, что такое возможно лишь при n=1 и при n=4. В каждом из этих случаев несложно найти k. При n=1 имеем k=6, а при n=4 имеем k=2.
Заметим, что мы пока не доказали, что оба эти случая реализуются. Ведь равенство площадей есть лишь необходимое условие для существования способа разрезания, но никак не достаточное (например, прямоугольник размера 1×6, очевидно, нельзя разрезать на два трехклеточных уголка, хотя 3·2=6). Для завершения доказательства следует привести примеры разрезаний каждого типа. Это можно сделать многими разными способами. На рисунке приведен лишь один из них, а вы попробуйте придумать что-нибудь свое. Кстати, интересно было бы ответить на такой вопрос: а сколько всего разрезаний каждого типа существует? (Автор этих строк, к примеру, ответа на этот вопрос пока не знает).

В заключение еще раз подчеркнем, что полное решение этой задачи включает в себя два шага: нахождение возможных случаев и проверка того, что все они реализуются. Каждый из этих шагов по отдельности не является решением задачи!